Inference-Only Debate Experiments Using Math Problems
Work supported by MATS and SPAR. Code at https://github.com/ArjunPanickssery/math_problems_debate/.
Three measures for evaluating debate are
whether the debate judge outperforms a naive-judge baseline where the naive judge answers questions without hearing any debate arguments.
whether the debate judge outperforms a consultancy baseline where the judge hears argument(s) from a single “consultant” assigned to argue for a random answer.
whether the judge can continue to supervise the debaters as the debaters are optimized for persuasiveness. We can measure whether judge accuracy increases as the debaters vary in persuasiveness (measured with Elo ratings). This variation in persuasiveness can come from choosing different models, choosing the best of N sampled arguments for different values of N, or training debaters for persuasiveness (i.e. for winning debates) using RL.
Radhakrishan (Nov 2023), Khan et al. (Feb 2024), and Kenton et al. (July 2024) study an information-gap setting where judges answer multiple-choice questions about science-fiction stories whose text they can’t see, both with and without a debate/consultancy transcript that includes verified quotes from the debaters/consultant.
Past results from the QuALITY information-gap setting are seen above. Radhakrishnan (top row) finds no improvement to judge accuracy as debater Elo increases, while Khan et al. (middle row) and Kenton et al. (bottom row) do find a positive trend. Radhakrishnan varied models using RL while Khan et al. used best-of-N and critique-and-refinement optimizations. Kenton et al. vary the persuasiveness of debaters by using models with different capability levels. Both Khan et al. and Kenton et al. find that in terms of judge accuracy, debate > consultancy > naive judge for this setting.
In addition to the information-gap setting, consider a reasoning-gap setting where the debaters are distinguished from the judge not by their extra information but by their stronger ability to answer the questions and explain their reasoning. Kenton et al. run debates on questions from MMLU, TruthfulQA, PrOntoQA (logical reasoning), GQPA, and GSM8K (grade-school math). For the Elo-calculation experiments they use Gemini Pro 1.0 and Pro 1.5 judges with five debaters: Gemma7B, GPT-3.5, Gemini Pro 1.0, Gemini Pro 1.5 (all with best-of-N=1), and Gemini Pro 1.5 with best-of-N=4.
They find (top row) that debate slightly outperforms consultancy but outperforms the naive-judge baseline for only one of the four judges; they don’t find that more persuasive debaters lead to higher judge accuracy. We get similar results (bottom row), specifically by
Generating 100 wrong answers and proofs to GSM8K questions to create binary-choice questions.
Computing the judge accuracy in naive, consultancy, and single-turn debate settings using four judges (Llama2-7B, Llama3-8B, GPT-3.5 Turbo, and GPT-4o) and seven debaters (Claude-3.5 Sonnet, Claude-3 Sonnet, GPT-3.5 Turbo, GPT-4o, Llama2-13B, Llama2-7B, and Llama3-8B).
Generating Elo scores from round-robin matchups between the seven models, using the same method as Kenton et al.
We basically replicate the results. We find that
Debate doesn’t consistently outperform the naive-judge baseline, and only slightly outperforms the consultancy baseline.
The positive relationship between debater persuasiveness and judge accuracy seen in the information-gap setting doesn’t transfer to the reasoning-gap setting. (Results are shown below colored by debater rather than by judge).
We also find some evidence of a self-preference bias (Panickssery et al., Apr 2024) where debaters have a higher Elo rating when judged by similar models. The GPT-3.5 Turbo judge sides most often with the GPT-3.5 Turbo debater while the Llama2-7B judge sides most often with the Llama2-13B debater, and the two GPT-based judges rank Llama2-7B last while the two Llama-based judges don’t. Below is the rank order of the debaters’ Elo ratings for each of the four judges.
Sorted ratings for llama2_7b (descending):
['llama2_13b', 'claude35_sonnet', 'llama2_7b', 'gpt35_turbo', 'claude3_sonnet', 'llama3_8b', 'gpt4o']
Sorted ratings for llama3_8b (descending):
['claude3_sonnet', 'gpt35_turbo', 'llama2_13b', 'claude35_sonnet', 'llama3_8b', 'llama2_7b', 'gpt4o']
Sorted ratings for gpt35_turbo (descending):
['gpt35_turbo', 'claude3_sonnet', 'llama3_8b', 'claude35_sonnet', 'llama2_13b', 'gpt4o', 'llama2_7b']
Sorted ratings for gpt4o (descending):
['gpt35_turbo', 'claude3_sonnet', 'llama3_8b', 'claude35_sonnet', 'gpt4o', 'llama2_13b', 'llama2_7b']Appendix: Cross table of wins
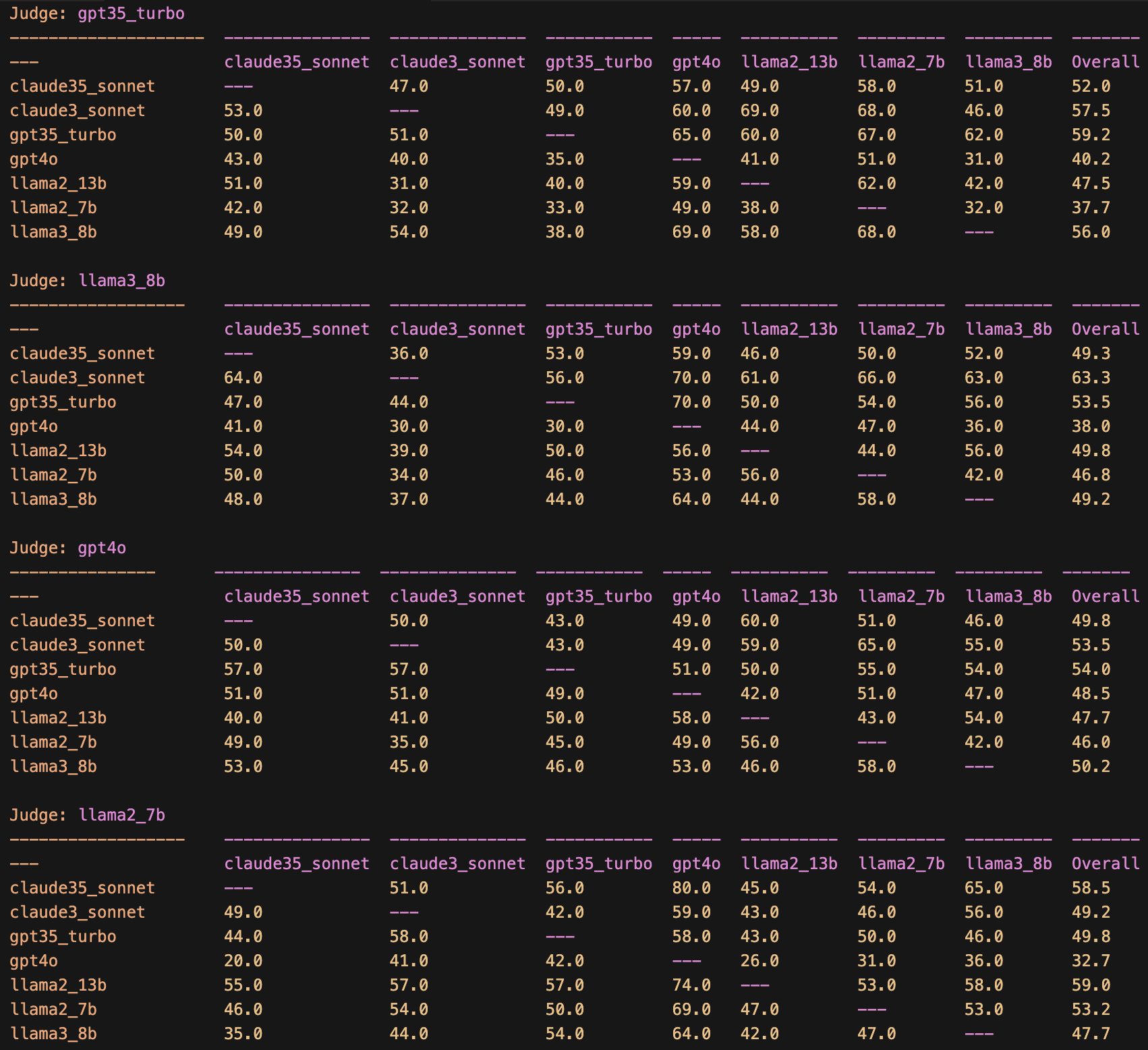
Cells show the win rate of the row-debater over the column-debater.
Executive summary: Experiments on AI debate for math problems show that debate only slightly outperforms consultancy and often fails to beat naive-judge baselines, with no clear relationship between debater persuasiveness and judge accuracy in reasoning-gap settings.
Key points:
Three measures for evaluating debate: comparison to naive-judge baseline, comparison to consultancy, and judge accuracy vs. debater persuasiveness.
Information-gap experiments (e.g., QuALITY) showed debate outperforming consultancy and naive judges, with positive trends in judge accuracy as debater persuasiveness increased.
Reasoning-gap experiments on math problems (GSM8K) found debate only slightly outperforming consultancy and often failing to beat naive-judge baselines.
No positive relationship observed between debater persuasiveness and judge accuracy in the reasoning-gap setting, contrary to information-gap results.
Evidence of self-preference bias where judges favor debaters from similar model families.
Results suggest limitations of current debate approaches for improving AI reasoning on math problems.
This comment was auto-generated by the EA Forum Team. Feel free to point out issues with this summary by replying to the comment, and contact us if you have feedback.