The proposal was written in collaboration with Aria Puri (ariapuri8@gmail.com)

If you have any questions, suggestions or ideas for collaboration to take this further, we’d love to hear so feel free to reach out at (bleddynmott@gmail.com)

Additionally, are currently looking for mentorship/guidance within the field of engineering/physics, particularly related to Effective Altruism, so we would love to talk if you have experience within this field.

Executive Summary

This research paper addresses the strategic deployment of refuge bunkers for nuclear winter, aiming to enhance logistics and efficacy through the development of a mathematical model that determines which locations are suitable for a bunker. The model, based on a multi-criteria evaluation approach, incorporates four critical parameters—population density, seismicity, shear strength of soil, and temperature—assigning weights based on their relative importance. Through the analysis of sample data, the paper evaluates the model’s applicability and effectiveness. The study also provides policy framework suggestions to ensure the successful execution of the model in determining optimal bunker locations, providing valuable insights for enhancing societal resilience in the event of a nuclear catastrophe.

I. THEORY

The concept of a nuclear winter refers to the climatic and environmental aftermath that follows a large-scale nuclear war, characterised by the injection of massive amounts of soot into the Earth’s stratosphere, blocking sunlight and causing a significant drop in temperatures. The resulting conditions could lead to widespread crop failure, food shortages, and devastating consequences for ecosystems and human societies.

Fig. 1. The ’Boom’ Analogy for Nuclear Weapon Use [1]

Civilisation resilience, on the other hand, encompasses efforts to both reduce the risk of civilisation collapse and enhance humanity’s ability to recover from such a collapse. This approach involves three primary defence layers: prevention, response, and resilience. Prevention focuses on averting the initiation of a catastrophe, while response aims to halt its escalation into a global catastrophe. Resilience addresses the question of how society can effectively cope in the aftermath of a widespread disaster, ensuring a capacity for recovery and rebuilding.

Fig. 2. The Three Layers of Defence of Catastrophic Risk [2]

Given the potential catastrophic consequences of a nuclear winter, bunkers serve as a key component in the response and resilience layers, safeguarding a portion of the population from immediate dangers and offering a foundation for recovery. Envisioned characteristics of bunkers, based on existing research, are a subterranean refuge a few metres below the ground, as that is enough distance to have suitable protection but also allow ease of exit in the case of collapse, offering a slight chance of survival rather than a certain death far below the soil. Many other considerations go into the bunker design, such as minimum viable population to sustain genetic diversity—with there being a range of values[3] from around 80 up to 160. Bunkers, designed with these criteria in mind, contribute significantly to the overall goal of enhancing civilisation resilience in the face of a nuclear catastrophe.

II. PROBLEM STATEMENT

In today’s complex geopolitical landscape, the proliferation of nuclear capabilities poses urgent challenges that require innovative solutions. China’s expanding nuclear arsenal introduces a “Three Body Problem,” disrupting orbital dynamics among major nuclear powers like the U.S. and Russia, challenging traditional deterrence strategies rooted in duels.

Advanced technologies, such as machine learning and artificial intelligence, bring both threats and opportunities to strategic stability, especially in the context of nuclear dynamics. Financial constraints worsen the situation, with major foundations withdrawing from the nuclear field, leaving a significant funding shortfall compared to other sectors.

The nuclear problem’s structure involves recognising the disproportionately devastating effects of large-scale nuclear wars and uncertainties in critical areas like nuclear winter science and escalation control. Deep uncertainty and unforeseen events add complexity, with constant concerns about accidents and potential rearming trends.

Historical precedence, exemplified by the Hiroshima and Nagasaki bombings, serves as a stark reminder of nuclear weapons’ catastrophic consequences. Recent geopolitical concerns, including Russia’s potential use of tactical nuclear weapons, highlight the persistent threat and the need for global risk mitigation.

Nuclear war’s potential for unprecedented devastation, including widespread loss of life, environmental devastation, and long-term health consequences, makes it a unique and interconnected global concern. The looming existential threat necessitates immediate attention, emphasising the urgency to address and mitigate this global risk.

III. LOCATION MODELLING

Model Overview: A Multi-Criteria Evaluation model will be used, resulting in a suitability index for each location that allows comparison between different locations. The first step in setting up this model will be choosing both the factors and constraints that will govern this model.

A. Assumptions

This model makes a number of assumptions due to the convolution that could be introduced by certain parameters. It is assumed that a full scale nuclear war has broken out, so the model does not include a parameter regarding distribution of the radioactive fallout to find a place that is potentially not radioactive, as the model is also meant to be able to be used in specific areas, not just finding the single best worldwide. Additionally, the lack of clear climate modelling as a result of nuclear winter means potential effects like flooding have not been included, however the model does include a parameter of temperature that demonstrates how they could be incorporated in future. Primarily, it is vital to reiterate the focus for this model is the best place for a bunker to survive the nuclear winter, rather than the best location for civilisational rebuilding which would have different factors.

B. Factors and Constraints

In the following, the definition of factors used will be “parameters for the model that express varying degrees of suitability for the decision under consideration”, and constraints will be the Boolean variables that “serve to delineate area not suitable for consideration”[4]. One factor from four key areas of social, geological, structural and weather have been chosen, based on what would have the greatest impact in that category and providing an example of how further, location specific parameters in each of these may be incorporated into the model.

1) Social—Population Density

For social parameters, the chosen factor is population density, which is measured in people per km^2, and will have a significant negative correlation with bunker suitability, as suggested by Turchin et al., (2019).[5] Firstly, as the model’s goal is to save only the 100-150 people required for the minimum bunker population, any increase in occupants would drastically decrease the chance of survival. Existing populations around the bunker would compete for resources, and hostile groups would attempt to gain access to the bunker in order to save themselves, jeopardising everyone’s chance of survival. Additionally, the population density will have a positive correlation to the chance of being a potential attack target—aggressors will likely look to inflict the most possible damage on a country.

2) Geological—Seismicity

In terms of potential geological impacts, earthquakes undeniably would inflict serious damage on the structural integrity of the bunker. To measure this as a parameter, the Gutenberg-Richter b-value is used, which expresses the relationship between the magnitude and total number of earthquakes in any given region and time period, and is a critical parameter for probabilistic estimation of seismic hazard.[6] Most importantly, it means only a single parameter is required for the incorporation of seismicity and hazard from earthquakes in the model, rather than both frequency and magnitude.

3) Structural—Shear Strength of Soil

Shear strength of the soil/rock that makes up the ground has been chosen as the primary structural factor of this model, and relates to the ability of the soil/rock to resist deformation under stress, measured in kPa within the model. Although shear strength is a good overall indicator of the ground’s suitability for construction to minimise risk of catastrophic structural failure, it is acknowledged that there are many more potential measures that could also be incorporated, which will be discussed at the end.

4) Weather—Temperature

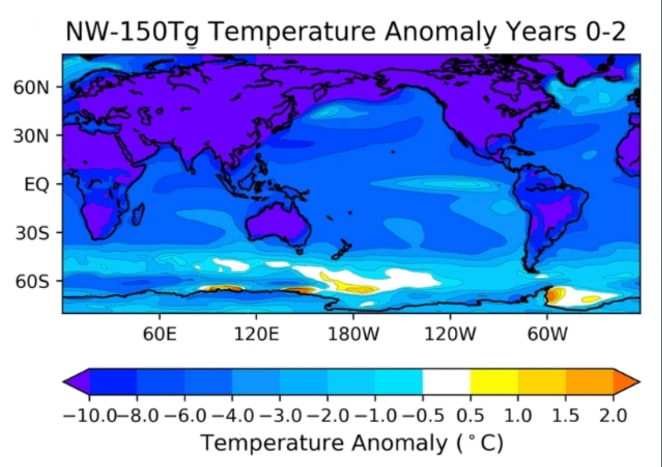
As described previously regarding the impact of nuclear winter, one of the major changes will be in climate, specifically the mean temperature drop globally. Modelling by Coupe et al. (2019)[7] simulates the injection of 150 Tg soot injection into the atmosphere, and has resulting data for the mean temperature anomaly, which varies across different regions in the world [See Figure Below]. Combining this and current mean temperature will create the predicted mean temperature, which is an important factor to consider—having temperatures too far from the ideal is likely to shorten the lifespan of occupants, as well as requiring far more energy to counteract, which may make long term survival impossible.

Fig. 3. Modelling by Coupe et al., 2019 [7]

5) Constraint—Blast Radius

A constraint applied to this model is that the location cannot be within the blast radius of likely targets, and is treated as a Boolean constraint rather than a factor as it is either inside or outside. Initially this model chooses the major cities within countries that have a nuclear weapon arsenal, as they would be likely targets and models blast radius based on the largest warhead currently in the US arsenal (the 1.2 Megatonne B-83) in order to future proof the model for further nuclear developments, using the NUKEMAP by Alex Wellerstein.[8] All locations within the thermal radiation radius of this warhead (13.2 km) are deemed unsuitable—a suitable bunker may still be within the “Light Blast Damage” radius outside this thermal radiation radius, but this would have negligible direct structural effects for a subterranean bunker, as only 1 psi of overpressure is expected, which correlates with the breaking of glass windows at a maximum.

C. Mathematical Modelling

Ultimately, the goal of this model is to compute a suitability index for each given location based on its specific values for the factors and constraints. This computation enables the ranking of locations, with higher indices indicating better suitability. The underlying principle guiding this model is the concept of a fuzzy set, which accommodates degrees of membership within a set, represented by a decimal value ranging from 0 to 1. This approach allows for the calculation of a suitability index and subsequent ranking of locations. The entire process involves four steps: standardisation, weighting, calculation, and decision-making, which may include an optional logic check.

D. Standardisation

For the constraint of blast radius, standardisation is simple due to its inherent Boolean property, and all that needs to be done is specify that:

Within the 1.2 Mt Thermal Radiation Radius = 0
Outside the 1.2 Mt Thermal Radiation Radius = 1

Membership functions must be formulated in order to best reflect the ideal behaviour of the factors, and their data distribution. A membership function is used to specify the degree to which a given input belongs to a set [9], by outputting the value for the degree of membership (between 0 and 1) discussed earlier.\par
In setting up membership functions, it is important to consider what input values should correspond with maximum suitability (1), which should correspond with minimum (0), and use these as anchor points of the function.

1) Population Density

For the consideration of population density, the selected membership function is $f (x) = e^{a - b x}$ (a general membership function form), chosen to illustrate the rapid decrease in suitability as population density increases, converging swiftly to 0 without intersecting. Specific values for $a$ and $b$ must be determined for this membership function. It is already established that $b$ should be negative, indicating that increasing population density decreases suitability.

Firstly, to ensure that the graph passes through the point (0, 1) when population density is zero (indicating maximum suitability), no adjustments are necessary as $e^{x}$ inherently satisfies this condition. Consequently, a = 0.

Secondly, the input value corresponding to the minimum suitability is chosen by identifying a potential target (through the process of identifying countries with nuclear arsenals) with the lowest population density. This ensures that the model considers the least suitable scenario, emphasising the importance of distance from potential targets. The lowest population density is found in Islamabad, which is approximately 2089 people per ${k m}^{2}$ . As the $e^{- x}$ function asymptotically approaches 0 but never intersects the x-axis, the chosen population input is when $e^{- b x} = e^{- 5}$ . The value 5 is commonly used in physics and modeling to represent completion. By comparing powers, b can be determined as b = $\frac{5}{2089}$ \approx 0.0025.

Fig. 4. Population Density Membership Function

2)Seismicity

For the seismicity factor, the sigmoidal function was selected due to its asymptotic behaviour towards both 0 and 1, providing a smooth curve between these points. The function is defined as

Research indicates that using the minimum and maximum raw factor values as anchor points for this function may not be appropriate. Instead, it is advisable to choose points where the factor begins to exert an effect and where the effect becomes negligible on suitability.[4]

In the context of seismicity, specific thresholds are relevant. Values less than 1.0 correspond to seismically active regions, while 2.0 tends to represent the least seismically active areas. Beyond these thresholds, the factor has little impact as the region is either highly active or not active. To accommodate this, the membership function should be adjusted so that these values align with the asymptotes.

To achieve this, anchor points are set at suitability values of 0.05 and 0.095, allowing for slight improvement beyond these points. Subsequently, these anchor points can be simultaneously solved for the parameters a and c to formulate the complete membership function.

3) Shear Strength of Soil

The shear strength factor also employs a sigmoidal membership function, given the well- defined boundaries for shear strength categorisations such as “Hard Ground” (150 kPa), deemed most suitable for construction, and “Very Soft Ground” (<40 kPa), considered entirely unsuitable. Similar to the previous approach, anchor points are established using these boundary values, with 140 kPa corresponding to a suitability of 0.95 and 40 kPa corresponding to a suitability of 0.05.

4) Temperature

The chosen membership function for temperature follows a Gaussian curve, capturing the idea that deviations from the ideal temperature make an environment less suitable. This is due to the increased energy requirements for heating or cooling, both of which come with adverse health effects.
The membership function is represented as

According to government research, the minimum temperature threshold for homes in winter is 18°C[10], set as the peak of the Gaussian curve where suitability is equal to 1.
Applying normal distribution principles, it is expected that 95% of the data falls within 2 standard deviations of the peak. Therefore, anchor points are set at a suitability index of 0.025 (2.5% in each tail). The input for this anchor point is chosen as 0°C based on the earlier anchor point principles, as further decreases from this temperature would have little additional impact on suitability due to already experiencing the full effects of freezing temperatures.
The mean (M) is set to 18°C, the peak of the curve, and solving the equation yields s = 6.62.

E. Weighting

After standardisation, the next crucial step involves assigning weights to each factor. This stage often introduces substantial bias and inconsistencies in terms of the weights’ interrelations. To address this issue, our model employs a pairwise comparison process developed by Saaty (1977)[11], known as the Analytical Hierarchy Process, for developing weights. In this process, each factor is systematically compared to every other factor on a 9-point reciprocal scale, as illustrated in the table specifically designed for this model (see below). One particularly challenging comparison was between seismicity and population density. However, population density was determined to be twice as important, given that locations with the potential for severe seismicity have already been accounted for through the membership functions. It is recommended to compute the weights from the pairwise comparison matrix using the principal eigenvector, a process implemented through computational programs in our model but can also be estimated through a variety of shorter processes.

Fig. 9. Resultant Weighting of Parameters

Consistency Ratio = 0.0079

Additionally, a consistency ratio can be calculated from the table that demonstrates how well the ratings align with each other in terms of a hierarchical order. For these weights, the consistency ratio = 0.0079, which does not need reevaluating according to Saaty (1977)[11] as it is below the 0.10 threshold.

F. Calculation

The Weighted Linear Combination is initially employed, involving the summation of the product of each factor’s standardised value and its corresponding weight. While this yields a suitability index, it necessitates the application of a Boolean constraint. The calculation of this constraint involves a T-Norm, a method for determining values at the intersection of two fuzzy sets.

Multiplying the Boolean value by the suitability index ensures that suitable locations remain unchanged, while unsuitable ones are set to 0. This is illustrated in the provided formula, where the sum of the weight multiplied by the standardised score is further multiplied by the Boolean constraint, resulting in the final suitability index.

The earlier introduction of the Weighted Linear Combination introduces the concept of trade-off, where a low score on one factor can be offset by a high score on another.[4] However, in the ultimate calculation involving the Boolean constraint and an intersection T-norm, there is no trade-off. This ensures that an unsuitable score for blast radius renders the entire location unsuitable, without the possibility of compensation by any other factor.

G. Decision-Making

The presentation and decision-making process for the final data can vary based on the data and format used.

Spatial coincidence offers one approach, involving overlaying map layers with different colours, akin to the steps in the Weighted Linear Combination (WLC). This visually highlights the most suitable areas. Alternatively, the final suitability index can be directly calculated, and areas can be shaded accordingly, as demonstrated in our example.

Once the suitability index is established, an efficient computational method for decision-making involves ranking the locations. Fulfilling any area demand, such as selecting the top 10 locations, becomes straightforward by starting with the highest-ranked locations and working down the list.

H. Logic-Check

Finally, it is advisable to conduct a logic check on the final ranking to address any parameters not considered in the model. For instance, if the ranking suggests an ideal location that is inherently inaccessible, and accessibility is not a parameter within the model, such results can be excluded from consideration. Recognising that no model can comprehensively cover all factors, this logic check ensures that the final rankings align with practical considerations.

IV. ANALYSIS

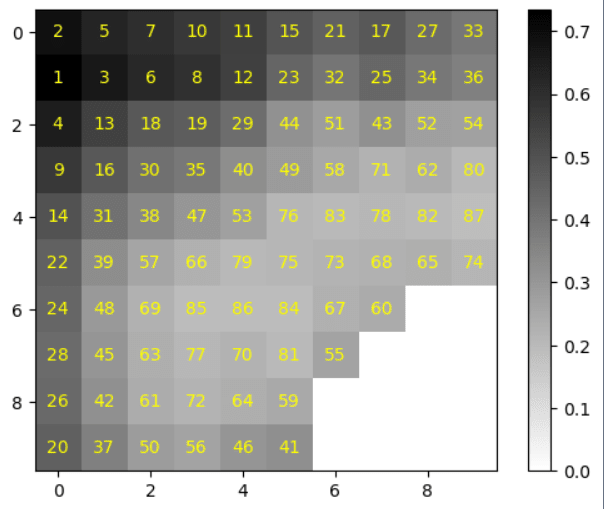
The model was used to analyse a 10 x 10 sample grid of raw data (refer to APPENDIX I). The values underwent weighting and processing, as illustrated in Figure X. Subsequently, the resultant suitability values were translated into a grayscale map using python (refer to APPENDIX II), emulating the data presentation format commonly used in GIS software as shown in the figure below. The cells were ranked, indicated by the number within the cell, with rank 1 being the most optimal location for bunker placement. As seen, preliminary testing would suggest the model can successfully identify areas suitable for a nuclear refuge, how further testing is required.

Fig. 10. Map of Suitability of Sample Data

V. Theory of Change

A. Impact

Amid global challenges, nuclear war stands among the top three most pressing issues, according to 80,000 Hours.[13] Our work focuses on the resilience stage, con- tributing to preparing for and mitigating potential fallout scenarios. The “Pragmatic Preservation” approach aims to save 1% of the global population after a nuclear catastrophe,[14] recognising the challenges in preventing nuclear war entirely. Additionally, our project aims for immediate impact and recovery by preserving the minimum viable population in each bunker. This approach provides an essential opportunity for humanity to recover and rebuild after a catastrophic nuclear event for the first 100 years post- catastrophe, acknowledging the urgency of the situation and ethical considerations surrounding potential consequences.

B. Tractability

1) Creating a Tractable Model

Instead of conducting a region-by-region analysis, we found feasibility in developing a mathematical model grounded in the fundamental principles of geography and engineering.

Ease of Implementation: The model is designed with simplicity and practicality in mind, making it straightforward to implement. Its structure allows for easy application by larger authorities equipped with extensive databases, streamlining the decision-making process for bunker site allocation.
Reasonable Assumptions: The model is built on well- founded assumptions, enhancing its reliability and reducing complexity. This ensures that decision-makers can trust the outputs of the model as it navigates through the intricate considerations involved in identifying suitable bunker locations.
Flexibility and Adaptability: The model’s flexibility allows for the customisation of weights and factors, catering to the specific needs and nuances of different regions. This adaptability enhances its utility, making it a versatile tool that can be fine-tuned for diverse geographical settings.

2) Alignment with Long-Term Goals:

This project aligns seamlessly with our career ambitions in engineering and physics. Both disciplines heavily involve mathematical modelling as a cornerstone for problem-solving. For instance, in engineering, modelling structural integrity or fluid dynamics relies on advanced mathematical frameworks to derive solutions. It provides an opportunity to develop crucial skills in data analysis, GIS software utilisation, and the critical assessment of database reliability. These skills are not only fundamental in our current project but also form the bedrock of numerous STEM-related fields. Given our keen interest in mathematics, we aspire to enhance our model by implementing more technical and potentially more accurate mathematical models.

Looking ahead, we aim to delve into research, whether in private ventures or academia. We envision reaching out to high-impact engineers and researchers for collaboration, thereby expanding the scope and impact of our project. The ultimate goal is to contribute valuable insights and tools to authorities involved in decision-making processes.

C. Neglect

Interaction with a high-impact engineer specialising in nuclear bunker design highlighted a significant gap in research focus. Extensive work has been done on construction and design, but strategic planning and logistics lack attention.

A comprehensive literature review unveiled a neglect in the field. Most papers briefly touch on parameters for bunker placement or perform rudimentary subjective comparisons between regions.

Existing research often explores survival on islands during nuclear winter but tends to focus on food-related aspects rather than specific bunker planning. Our project fills this gap by offering a comprehensive model for strategic and optimal bunker locations.

VI. LOGISTICS AND POLICY

A. Exclusion of Parameters

The exclusion of certain parameters in our model is driven by specific considerations. For instance, variables like wind and precipitation were omitted due to their non-uniform variations in a global nuclear winter sce- nario, where comprehensive global predictions are cur- rently unavailable. Additionally, soil fertility and energy considerations were excluded, as our model is designed to prioritise the survival of humanity rather than the reestablishment of civilisation. Notably, the latter would necessitate a distinct model, where the optimal locations identified by our model could potentially serve as valuable input for further analysis.

B. Integrated Policy Framework for Bunker Logistics

Secrecy as a Key Element: The policy implications for bunker installation emphasise the critical necessity of maintaining secrecy regarding bunker locations. This measure is deemed essential to prevent unauthorised access by the public, given the finite capacity of bunkers, and potential interference from international governments, such as targeting bunker sites alongside metropolitan cities during nuclear war.
International Collaboration for Optimal Placement: The proposed policy framework explores the possibility of international cooperation in determining bunker locations. This collaboration could involve placing bunkers in foreign less-developed territories, facilitated by more developed nations contributing resources for construction and maintenance. This approach optimises resource utilisation and contributes to the overall resilience of bunker systems, particularly when more developed nations lack secure locations for local bunker installations.
Military Involvement for Enhanced Security: The policy also considers the potential involvement of the military in bunker-related initiatives. This involves exploring the proximity of bunkers to military bases, enhancing security measures and readiness, especially in the context of geopolitical uncertainties and potential wartime scenarios. The strategic placement of bunkers near military installations aims to ensure the safety and security of these critical infrastructure elements.
Sustainability and Long-Term Resilience: While not directly related to our project, it is evident that for the success of the model, authorities must deliberate on the ideal size and quantity of bunkers, alongside their placement. Moreover, a minimum viable population should be maintained in proximity to the bunker at all times, potentially engaging in research or military operations, with the option for rotation over time, accounted for by the deliberate neglect of ease-of-access constraints in our model.

VII. CONCLUSION

This research offers a methodical approach to bunker location modeling, employing a Multi-Criteria Evaluation model and examining factors like population density, seismicity, soil strength, and temperature. The subsequent steps of weighting, calculation, and decision-making con- tribute to a comprehensive evaluation, concluding with a logic check for practical relevance. The Theory of Change emphasises potential impact, feasibility, and addressing gaps in strategic bunker planning. The proposed logistics and policy considerations underscore the need for international collaboration, military involvement, and sustainable long-term resilience planning. Overall, this study aims to provide a scientific framework for addressing the complex challenges posed by the looming threat of nuclear catastrophe. Further improvements are necessary to increase the effectiveness of the model, including incorporation of more parameters and more thorough testing, however the intention of this is a preliminary, proof of concept model for the goals outlined.

References

[1] Sean Lawrence (2023). How Engineers Can Work On Civilisation Resilience. Available: https://www.highimpactengineers.org/ how- engineers- can- work- on- civilisation- resilience

[2] Owen Cotton-Barratt, Max Daniel, Anders Sandberg (2020). Defence in Depth Against Human Extinction: Prevention, Response, Resilience, and Why They All Matter. Available: https://onlinelibrary.wiley.com/doi/full/10.1111/ 1758- 5899.12786

[3] Damian Carrington (2022). “Magic number” for space pioneers cal- culated. Available: https://www.newscientist.com/article/ dn1936- magic- number- for- space- pioneers- calculated/#. VBiC_XtDLwo

[4] J R Eastman (1999). 35 Multi-criteria evaluation and GIS. Available:
https://www.geos.ed.ac.uk/~gisteac/gis_book_abridged/
files/ch35.pdf

[5] Turchin, A., Green, B. (2019). Islands as refuges for surviving global catastrophes. Available: https://www.researchgate.net/publication/327448865_Islands_as_refuges_for_ surviving_global_catastrophes

[6] G-M Geffers, I G Main, M Naylor (2022). Biases in estimating b-values from small earthquake catalogues: how high are high b-values? Available: https://academic.oup.com/gji/article/ 229/3/1840/6515950

[7] Coupe et al (2019). Nuclear Niño response observed in simulations of nuclear war scenarios. Available: https://www.nature.com/ articles/s43247- 020- 00088- 1

[8] Alex Wellerstein (2023). NUKEMAP. Available: https: //nuclearsecrecy.com/nukemap/

[9] Dr Qadri Hamarsheh. Neural Networks and Fuzzy Logic. Available: https://www.philadelphia.edu.jo/academics/qhamarsheh/uploads/Lecture%2018_Different%20Types% 20of%20Membership%20Functions%201.pdf

[10] Rachel Wookey, Dr. Angie Bone, Catriona Carmichael, Anna Crossley (2014). Minimum home temperature thresholds for health in winter. Available: https://assets.publishing.service. gov.uk/government/uploads/system/uploads/attachment_ data/file/776497/Min_temp_threshold_for_homes_in_ winter.pdf

[11] Thomas L Saaty (1997). A scaling method for priorities in hier- archical structures. Available: https://www.sciencedirect.com/ science/article/abs/pii/0022249677900335

[12] Christian Ruhl (2023). Global Catastrophic Nu-
clear Risk: A guide for philanthropists. Avail-
able: https://www.founderspledge.com/research/ global- catastrophic- nuclear- risk- a- guide- for- philanthropists

[13] Benjamin Hilton, Peter McIntyre (2022). Nuclear War. Available: https://80000hours.org/problem- profiles/ nuclear- security/

[14] Derek Parfit (1984). Reasons and Persons. Available: https:// academic.oup.com/book/12484

Location Modelling for Post-Nuclear Refuge Bunkers