New report on how much computational power it takes to match the human brain (Open Philanthropy)

Written by Joseph Carlsmith.

Open Philanthropy is interested in when AI systems will be able to perform various tasks that humans can perform (“AI timelines”). To inform our thinking, I investigated what evidence the human brain provides about the computational power sufficient to match its capabilities. I consulted with more than 30 experts, and considered four methods of generating estimates, focusing on floating point operations per second (FLOP/s) as a metric of computational power.

The full report on what I learned is here. This blog post is a medium-depth summary of some context, the approach I took, the methods I examined, and the conclusions I reached. The report’s executive summary is a shorter overview.

In brief, I think it more likely than not that 10¹⁵ FLOP/s is enough to perform tasks as well as the human brain (given the right software, which may be very hard to create). And I think it unlikely (<10%) that more than 10²¹ FLOP/s is required. (1) But I’m not a neuroscientist, and the science here is very far from settled. (2) I offer a few more specific probabilities, keyed to one specific type of brain model, in the report’s appendix.

For context: the Fugaku supercomputer (~$1 billion) performs ~4×10¹⁷ FLOP/s, and a V100 GPU (~$10,000) performs up to ~10¹⁴ FLOP/s. (3) But even if my best guesses are right, this doesn’t mean we’ll see AI systems as capable as the human brain anytime soon. In particular: actually creating/training such systems (as opposed to building computers that could in principle run them) is a substantial further challenge.

Context

Some classic analyses of AI timelines (notably, by Hans Moravec and Ray Kurzweil) emphasize forecasts about when available computer hardware will be “equivalent,” in some sense (see below for discussion), to the human brain. (4)

*Graph schema for classic forecasts. See real examples* *here* *and* *here*.

A basic objection to predicting AI timelines on this basis alone is that you need more than hardware to do what the brain does. (5) In particular, you need software to run on your hardware, and creating the right software might be very hard (Moravec and Kurzweil both recognize this, and appeal to further arguments). (6)

In the context of machine learning, we can offer a more specific version of this objection: the hardware required to run an AI system isn’t enough; you also need the hardware required to train it (along with other resources, like data). (7) And training a system requires running it a lot. DeepMind’s AlphaGo Zero, for example, trained on ~5 million games of Go. (8)

Note, though, that depending on what sorts of task-performance will result from what sorts of training, a framework for thinking about AI timelines that incorporated training requirements would start, at least, to incorporate and quantify the difficulty of creating the right software more broadly. (9) This is because training turns computation and data (along with other resources) into software you wouldn’t otherwise know how to code directly.

What’s more, the hardware required to train a system is related to the hardware required to run it. (10) This relationship is central to Open Philanthropy’s interest in the topic of this report, and to an investigation my colleague Ajeya Cotra has been conducting, which draws on my analysis. That investigation focuses on what brain-related FLOP/s estimates, along with other estimates and assumptions, might tell us about when it will be feasible to train different types of AI systems. I don’t discuss this question here, but it’s an important part of the context. And in that context, brain-related hardware estimates play a different role than they do in forecasts like Moravec’s and Kurzweil’s.

Approach

I focus on floating point operations per second (FLOP/s) as a metric of computational power. These are arithmetic operations (addition, subtraction, multiplication, division) performed on a pair of numbers represented in a computer in a format akin to scientific notation. Performing tasks with computers requires resources other than FLOP/s (for example, memory and memory bandwidth), so this focus is narrow (see section 1.4 for more discussion). But FLOP/s are a key input to the investigation of training costs described above; and they’re one important resource more generally.

My aim in the report is to see what evidence the brain provides about what sorts of FLOP/s budgets would be enough to perform any cognitive task that the human brain can perform. (11) Section 1.6 gives more details about the tasks I have in mind.

The project here is related to, but distinct from, directly estimating the minimum FLOP/s sufficient to perform any task the brain can perform. Here’s an analogy. Suppose you want to build a bridge across the local river, and you’re wondering if you have enough bricks. You know of only one such bridge (the “old bridge”), so it’s natural to look there for evidence. If the old bridge is made of bricks, you could count them. If it’s made of something else, like steel, you could try to figure out how many bricks you need to do what a given amount of steel does. If successful, you’ll end up confident that e.g. 100,000 bricks is enough to build such a bridge, and hence that the minimum is less than this. But how much less is still unclear. You studied an example bridge, but you didn’t derive theoretical limits on the efficiency of bridge-building. (12)

The project is also distinct from estimating the FLOP/s “equivalent” to the human brain. As I discuss in the report’s appendix, I think the notion of “the FLOP/s equivalent to the brain” requires clarification: there are a variety of importantly different concepts in the vicinity.

To get a flavor of this, consider the bridge analogy again, but assume that the old bridge is made of steel. What number of bricks would be “equivalent” to the old bridge? The question seems ill-posed. It’s not that bridges can’t be built from bricks. But we need to say more about what we want to know.

I group the salient possible concepts of the “FLOP/s equivalent to the human brain” into four categories, each of which, I argue, has its own problems (see section 7.5 for a summary chart). In the hopes of avoiding some of these problems, I have kept the report’s framework broad. The brain-based FLOP/s budgets I’m interested in don’t need to be uniquely “equivalent” to the brain. Nor need they accommodate any further constraints on the similarity between brain’s internal dynamics and those of the AI systems under consideration (see section 7.2); or on the training/engineering processes that could create such systems (see section 7.3). The budgets just need to be big enough, in principle, to perform the tasks in question.

Methods

I considered four methods of using the brain to generate FLOP/s budgets. They were:

Estimate the FLOP/s required to model the brain’s low-level mechanisms at a level of detail adequate to replicate task-performance (the “mechanistic method”). (13)
Identify a portion of the brain whose function we can approximate with computers, and then scale up to FLOP/s estimates for the whole brain (the “functional method”).
Use the brain’s energy budget, together with physical limits set by Landauer’s principle, to upper-bound required FLOP/s (the “limit method”).
Use the communication bandwidth in the brain as evidence about its computational capacity (the “communication method”). I discuss this method only briefly.

All these methods must grapple in different ways with the severe limits on our understanding of how the brain processes information – a consistent theme in my conversations with experts. Section 1.5.1 details some of the limits I have in mind. In many cases, central barriers include:

we lack the tools to gather the data we need (for example, we can’t reliably measure the input-output transformation a neuron implements during live behavior), (14) and/or
we don’t know enough about the tasks that cells or groups of cells are performing to tell how different lower-level mechanisms contribute. (15)

These and other barriers counsel pessimism about the robustness of FLOP/s estimates based on our current neuroscientific understanding (see section 1.2 for further caveats). But the aim here is not to settle the question: it’s to make reasonable best-guesses, using the inconclusive evidence currently available.

I’ll say a few words about each method in turn, and the numbers that result.

The mechanistic method

The mechanistic method attempts to estimate the computation required to model the brain’s biological mechanisms at a level of detail adequate to replicate task-performance. This method receives the most attention in the report, and it’s the one I put most weight on.

Simulating the brain in extreme detail would require enormous amounts of computational power. (16) The central question for the mechanistic method, then, is which details need to be included, and which can be left out or summarized.

The approach I pursue focuses on signaling between cells. Here, the idea is that for a process occurring in a cell to matter to task-performance, it needs to affect the type of signals that cell sends to other cells. Hence, a model of that cell that replicates its signaling behavior (that is, the process of receiving signals, “deciding” what signals to send out, and sending them) would replicate the cell’s role in task-performance, even if it leaves out or summarizes many other processes occuring in the cell. Do that for all the cells in the brain involved in task-performance, and you’ve got a model that can match the brain’s capabilities. (17)

I give a basic overview of the signaling processes in the brain in section 1.5. For the purposes of the mechanistic method, I divide these into three categories:

Standard neuron signaling. This is the form of signaling in the brain that receives the most attention from neuroscientists and textbooks. In brief: cells called neurons signal to each other using electrical impulses called action potentials or spikes. These action potentials travel down a tail-like projection called an axon, which branches off to form connections called synapses with other neurons. When an action potential from one neuron reaches the synapse between that neuron and another, this can cause the first neuron to release chemicals called neurotransmitters, which in turn cause changes in the second neuron that influence whether it fires. These changes can proceed in part via activity in the neuron’s dendrites – tree-like branches that typically receive signals from other neurons. I use the term spike through synapse to refer to the event of a spike arriving at a synapse.
Learning. Experience shapes neural signaling in a manner that improves task-performance and stores task-relevant information. (18) Where not already covered by (1), I bucket the processes involved in this under “learning.” Salient examples include: changes at synapses that occur over time, other changes to the electrical properties of neurons, and the growth and death of neurons and synapses.
Other signaling mechanisms. The brain contains a wide variety of signaling mechanisms (or candidate mechanisms) other than those included in the basic picture of standard neuron signaling. These include other types of chemical signals, other types of cells, synapses that don’t work via neurotransmitter release, local electric fields, and other forms of signaling along the axon. Where not already covered by (1) and (2), I lump all of these, known and unknown, under “other signaling mechanisms.”

Here’s a diagram of the basic framework I use for thinking about what models of these processes need to capture:

Here’s the mechanistic method formula that results:

Total FLOP/s = FLOP/s for standard neuron signaling +
FLOP/s for learning +
FLOP/s for other signaling mechanisms

I’m particularly interested in the following argument:

You can capture standard neuron signaling and learning with somewhere between ~10¹³-10¹⁷ FLOP/s overall.
This is the bulk of the FLOP/s burden (other signaling mechanisms may be important to task-performance, but they won’t require comparable FLOP/s to capture).

Why think (I)? In brief: there are roughly 10¹¹ neurons in the brain, and roughly 10¹⁴-10¹⁵ synapses. On the estimates that seem most plausible to me, each neuron spikes about 0.1-1 times per second (this is lower than the rate assumed by many other mechanistic method estimates in the literature), (19) suggesting ~10¹³-10¹⁵ spikes through synapses per second overall. (20) So 10¹³-10¹⁷ FLOP/s budgets:

1-100 FLOP per spike through synapse, which would cover various simple models of the impact of a spike through synapse on the downstream neuron (~1 FLOP per spike through synapse), with two extra orders of magnitude to allow for some possible complexities. (21)
100-1,000,000 FLOP/s per neuron, (22) which covers a variety of simplified models of a neuron’s “decision” about whether to fire (including some that incorporate computation taking place in dendrites) that various arguments suggest would be adequate, and which, at the high end, covers a level of modeling complexity (single-compartment Hodgkin-Huxley models) (23) that I expect many computational neuroscientists to think unnecessary. (24)

The FLOP/s budgets for learning are a significant source of uncertainty, but various models of learning in the brain plausibly fall within this range as well; and there are some additional reasons – for example, reasons related to the timescales of processes involved in learning – that we might think that learning will require fewer FLOP/s than standard neuron signaling. Various experts I spoke to (though not all) were also sympathetic towards (I). (25)

What about the other signaling mechanisms at stake in (II)? Here, the question is not whether these mechanisms matter. The question is whether they meaningfully increase a FLOP/s budget that already covers standard neuron signaling and learning. My best guess is that they don’t. This is mostly because:

My impression is that most experts who have formed opinions on the topic (as opposed to remaining agnostic) do not expect these mechanisms to account for the bulk of the brain’s information-processing, even if some play an important role. (26)
Relative to standard neuron signaling, each of the mechanisms I consider is some combination of (a) slower, (b) less spatially-precise, (c) less common in the brain (or, not substantially more common), or (d) less clearly relevant to task-performance.

Section 2.3 offers an initial examination of a number of these mechanisms in light of considerations like (a)-(d). See section 2.3.7 for a summary chart.

To be clear: many of the questions at stake in these estimates remain very open. The models and assumptions covered by 10¹³-10¹⁷ FLOP/s seem to me reasonable defaults given what we know now. But there are also a variety of ways in which these numbers could be too low, or too high.

In particular, numbers larger than 10¹⁷ FLOP/s might be suggested by:

Higher-precision temporal dynamics in the brain. (27)
Very FLOP/s-intensive deep neural network (DNN) models of neuron behavior (see the discussion in section 2.1.2.2 of Beniaguev et al. (2020) – a model that could suggest that you need ~10²¹ FLOP/s for the brain overall).
Estimates based on time-steps per relevant variable at synapses, instead of spikes through synapses per second (see discussion here).
Larger FLOP/s budgets for processes like dendritic computation and learning. (28)
Higher estimates of parameters like synapse count or average firing rate. (29)
Background expectations that information-processing in biology will be extremely complex, efficient, and/or ill-suited to replication using digital computer hardware. (30)

Numbers smaller than 10¹³ FLOP/s might be suggested by:

Noise, redundancy, and low-dimensional behavior amongst neurons, which suggest that modeling individual neurons/synapses might be overkill.
Overestimates of FLOP/s capacity that result from applying analogs of the mechanistic method to human-engineered computers.
Evolutionary constraints on the brain’s design (e.g., constraints on volume, energy consumption, growth/maintenance requirements, genome size, and speed/reliability of basic elements, as well as an inability to redesign the system from scratch), which suggest the possibility of improvements in efficiency.

Overall, I find the considerations pointing to the adequacy of budgets smaller than 10¹³-10¹⁷ FLOP/s more compelling than the considerations pointing to the necessity of larger ones (though it also seems easier, in general, to show that X is sufficient than that X is strictly required – an asymmetry present throughout the report). But the uncertainties in either direction rightly prompt dissatisfaction with the mechanistic method’s robustness.

The functional method

The functional method attempts to identify a portion of the brain whose function we can approximate with artificial systems, and then to scale up to an estimate for the brain as a whole.

Various attempts at this method have been made. I focus on two categories: estimates based on the retina, and estimates based on the visual cortex.

The retina

The retina is a thin layer of neural tissue in the eye. It performs the first stage of visual processing, and sends the results to the rest of the brain via spike patterns in the optic nerve – a bundle of roughly a million axons of neurons called retinal ganglion cells.

I consider two types of estimates for the FLOP/s sufficient to replicate retinal function.

Hans Moravec estimates 10⁹ calculations per second, based on the assumption that the retina’s function is to detect edges and motion. (31) One problem here is that the retina does a lot more than this (for example, it can anticipate motion, it can signal that a predicted stimulus is absent, and it can adapt to different lighting conditions). (32)
Recent deep neural networks used to predict ganglion cell firing patterns suggest higher estimates: ~10¹³-10¹⁴ FLOP/s (though I’m very uncertain about these numbers, as they depend heavily on the size of the visual input, and on how these models would scale up to a million ganglion cells). (33) These, too, do not yet represent full replications of human retinal computation, but they outperform various other models on natural images. (34)

Moving from the retina to the whole brain introduces further uncertainty. There are a variety of possible ways of scaling up (e.g., based on mass, volume, neurons, synapses, and energy use), which result in scaling factors between 10³ and 10⁶. (35) These factors imply the following ranges for the whole brain:

Using Moravec’s retina estimate: 10¹²-10¹⁵ calculations per second
Using DNN retina model estimates: 10¹⁶-10²⁰ FLOP/s

But there are also differences between the retina and the rest of the brain, which weaken the evidence these numbers provide (for example, the retina is less plastic, more specialized, and subject to unique physical constraints).

Overall, I treat the DNN estimates here as some weak evidence that the mechanistic method range above (10¹³-10¹⁷ FLOP/s) is too low (and these could yet underestimate the retina’s complexity, or the complexity of the brain relative to the retina). But as noted, I feel very unsure about the estimates themselves. And it seems plausible to me that the relevant models use many more FLOP/s than are required to automate what ganglion cells do (for example, these models reflect specific implementation choices that haven’t been shown necessary; and Moravec’s estimate, even if incomplete in its coverage of all retinal computation, is much lower – see the end of section 3.1.2 for more discussion).

The visual cortex

A different application of the functional method treats deep neural networks trained on vision tasks as automating some portion of the information-processing in the visual cortex – the region of the brain that receives and begins to process visual signals sent from the retina (via the lateral geniculate nucleus). (36)

Such networks can classify full-color images into 1000 different categories with something like human-level accuracy. (37) What’s more, they can be used as state-of-the-art predictors of neural activity in the visual cortex, and the features they detect bear interesting similarities to ones the visual cortex detects (see section 3.2 for discussion).

Using these networks for functional method estimates, though, introduces at least two types of uncertainty. First, there’s clearly a lot happening in the visual cortex other than image classification of the type these models perform. For example: the visual cortex is involved in motor processing, prediction, and learning. Indeed, the idea that different cortical regions are highly specialized for particular tasks seems to have lost favor in neuroscience. And vision as a whole seems closely tied to, for example, behavioral affordances, 3D models of an environment, and high-level interpretations of what’s significant. (38)

Second, even on the particular task of image classification, available DNN models do not yet clearly match human-level performance. For example:

They’re vulnerable to adversarial examples and other types of generalization failures.
They typically use smaller inputs than the visual cortex receives.
They classify stimuli into a smaller number of categories (indeed, it is unclear to me, conceptually, how to bound the number of categories humans can recognize).

*Examples of generalization failures. From* *Geirhos et al. (2020)*, Figure 3, p. 8, reprinted with permission, and unaltered. Original caption: “Both human and machine vision generalise, but they generalise very differently. Left: image pairs that belong to the same category for humans, but not for DNNs. Right: image pairs assigned to the same category by a variety of DNNs, but not by humans.”

Suppose we try to forge ahead with a functional method estimate, despite these uncertainties. What results?

An EfficientNet-B2 takes 10⁹ FLOP to classify a single image (though it may be possible to use even less than this). (39) Humans can recognize ~ten images per second; running an EfficientNet-B2 at this frequency would require ~10¹⁰ FLOP/s. (40)

I estimate that the primary visual cortex (a large and especially well-studied part of the early visual system, also called V1) is ~.3-3% of the brain’s neurons, and that visual cortex as a whole is ~1-10% (though if we focused on percentage of volume, mass, energy consumption, or synapses, the relevant percentages might be larger). (41)

We also need to estimate two other parameters, representing the two categories of uncertainty discussed above:

The percentage of the visual cortex’s information-processing capacity that it devotes to tasks analogous to image classification, when it performs them. (42)
The factor increase in FLOP/s required to reach human-level performance on this task (if any), relative to the FLOP/s costs of an EfficientNet-B2 run at 10 Hz.

My estimates for these are very made-up. For (1), I use 1% of V1 as a more conservative estimate, and 10% of the visual cortex as a whole as a more aggressive one, with 1% of the visual cortex as a rough middle. For (2), I use 10× as a low end, and 1000× as a high end, with 100× as a rough middle. See section 3.2.3 for a bit more discussion of these numbers.

Combining these estimates for (1) and (2), we get:

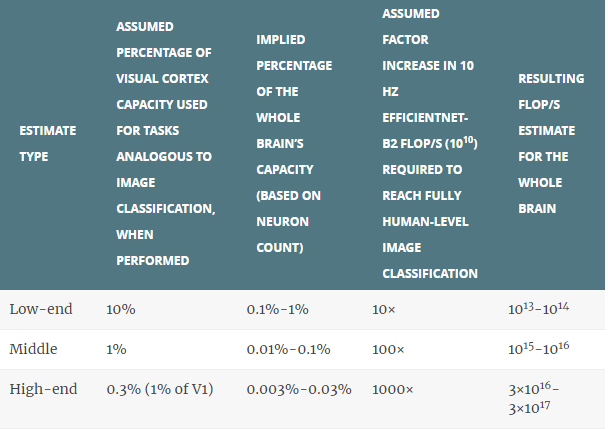
Overall, I hold these estimates very lightly. The question of how high (2) could go, for example, seems very salient. And the conceptual ambiguities involved in (1) caution against relying on what might appear to be conservative numbers. (43)

Still, I don’t think these estimates are entirely uninformative. For example, it is at least interesting to me that you need to treat a 10 Hz EfficientNet-B2 as running on e.g. ~0.1% of the FLOP/s of a model that would cover ~1% of V1, in order to get whole brain estimates substantially above 10¹⁷ FLOP/s – the top end of the mechanistic method range I discussed above. This weakly suggests to me that such a range is not way too low.

The limit method

The limit method attempts to upper bound required FLOP/s by appealing to physical limits.

I focus on limits imposed by “Landauer’s principle,” which specifies the minimum energy costs of erasing bits (see section 4.1.1 for more explanation). Standard FLOP (that is, those performed by human-engineered computers) erase bits, which means that an idealized computer running on the brain’s energy budget (~20W) can only perform so many standard FLOP/s: specifically, ~7×10²¹ (~10²¹ if we assume 8-bit FLOPs, and ~10¹⁹ if we assume current digital multiplier implementations). (44)

Does this upper bound the FLOP/s required to match the brain’s task-performance? Not on its own, because the brain need not be performing operations that resemble standard FLOPs. (45) Indeed, in theory, it appears possible to perform arbitrarily complicated computations with very few bit erasures, with manageable increases in computation and memory burden. (46)

Absent a simple upper bound, then, the question is what, if anything, we can say about the ratio between the FLOP/s required to match the brain’s task-performance and the maximum bits per second the brain can erase. Various experts I spoke to about the limit method (though not all) were quite confident that the latter far exceed the former. (47) They gave various arguments, which I group into:

Algorithmic arguments (section 4.2.1), which focus on the bits we should expect the brain’s “algorithm” to erase, per FLOP required to replicate it; and
Hardware arguments (section 4.2.2), which focus on the energy we should expect the brain’s hardware to dissipate, per FLOP required to replicate the computation it implements.

Of these, the hardware arguments seem to me stronger (though they also don’t seem to me to rely very directly on Landauer’s principle in particular). Both, though, appeal to general considerations that apply even if more specific assumptions from other methods are mistaken.

Overall, it seems unlikely to me that required FLOP/s exceeds the bounds suggested by the limit method. This is partly out of deference to various experts; partly because various algorithmic and hardware arguments seem plausible to me (regardless of whether they rely on Landauer’s principle or not); and partly because other methods generally point to lower numbers. But this doesn’t seem like a case of a physical limit imposing a clean upper bound.

The communication method

The communication method attempts to use the communication bandwidth in the brain as evidence about its computational capacity.

Communication bandwidth, here, refers to the speed with which a system can send different amounts of information different distances. This is distinct from the operations per second it can perform (computation). But estimating communication bandwidth might help with computation estimates, because the marginal value of additional computation and communication are related (e.g., too little communication and your computational units sit idle; too few computational units and it becomes less useful to move information around).

The basic form of the argument is roughly:

The communication bandwidth in the brain is X.
If the communication bandwidth in the brain is X, then Y FLOP/s is probably enough to match the brain’s task-performance.

I don’t examine attempts to use this method in any detail. But I note some examples in the hopes of inspiring future work.

Dr. Paul Christiano, one of Open Philanthropy’s technical advisors, offers a loose estimate of the brain’s communication capacity, and suggests that it looks comparable (indeed, inferior) to the communication profile of a V100 GPU. Perhaps, then, the brain’s computational capacity is comparable (or inferior) to a V100 as well. (48) This would suggest 10¹⁴ FLOP/s or less for the brain (though I think this argument gets more complicated if you also bring in comparisons based on memory and energy consumption).
AI Impacts recommends using traversed edges per second (TEPS) – a metric used to assess communication capabilities of human-engineered computers, which measures the time required to perform a certain type of search through a random graph – to quantify the brain’s communication capacity. (49) Treating spikes through synapses as traversals of an edge, they estimate ~2×10¹³-6×10¹⁴ TEPS for the brain. They then examine the ratio of TEPS to FLOP/s in eight top supercomputers, and find a fairly consistent ~500-600 FLOP/s per TEPS. Scaling up from their TEPS estimate for the brain, they get ~10¹⁶-3×10¹⁷ FLOP/s.

I haven’t vetted these estimates. And in general, efforts in this vein face a number of issues (see section 5.2 for examples). But I think they may well prove helpful.

Conclusions

Here’s a chart plotting the different estimates I discussed, along with a few others from the report.

*The report’s main estimates. See the* *conclusion* *for a list that describes them in more detail, and summarizes my evaluation of each.*

As I’ve said, these numbers should be held lightly. They are back-of-the-envelope calculations, offered, in the report, alongside initial discussion of complications and objections. The science here is very far from settled.

Here’s a summary of the main conclusions discussed above:

Mechanistic estimates suggesting that 10¹³–10¹⁷ FLOP/s would be enough to match the human brain’s task-performance seem plausible to me. Some considerations point to higher numbers; some, to lower numbers. Of these, the latter seem to me stronger.
I give less weight to functional method estimates. However, I take estimates based on the visual cortex as some weak evidence that 10¹³–10¹⁷ FLOP/s isn’t much too low. Some estimates based on deep neural network models of retinal neurons point to higher numbers, but I take these as even weaker evidence.
I think it unlikely that the required number of FLOP/s exceeds the bounds suggested by the limit method. However, I don’t think the method itself airtight.
Communication method estimates may well prove informative, but I haven’t vetted them.

And remember, the minimum adequate budget could be lower than all these estimates. The brain is only one example of a system that performs these tasks.

Overall, I think it more likely than not that 10¹⁵ FLOP/s is enough to perform tasks as well as the human brain (given the right software, which may be very hard to create). And I think it unlikely (<10%) that more than 10²¹ FLOP/s is required. But there’s no consensus amongst experts.

I offer a few more specific probabilities, keyed to one specific type of brain model, in the appendix. My current best-guess median for the FLOP/s required to run that particular type of model is around 10¹⁵ (recall that none of these numbers are estimates of the FLOP/s uniquely “equivalent” to the brain).

As can be seen from the figure above, the FLOP/s capacities of current computers cover the estimates I find most plausible. However:

Task-performance requires resources other than FLOP/s (for example, memory and memory bandwidth).
Performing tasks on a particular machine can introduce further overheads and complications.
Most importantly, matching the human brain’s task-performance requires actually creating sufficiently capable and computationally efficient AI systems, and this could be extremely (even prohibitively) difficult in practice even with computers that could run such systems in theory. Indeed, as noted above, the FLOP/s required to run a system that does X can be available even while the resources (including data) required to train it remain substantially out of reach. And what sorts of task-performance will result from what sorts of training is itself a further, knotty question. (50)

So even if my best-guesses are correct, this does not imply that we’ll see AI systems as capable as the human brain anytime soon.

Acknowledgements

This project emerged out of Open Philanthropy’s engagement with some arguments suggested by one of our technical advisors, Dario Amodei, in the vein of the mechanistic and functional methods discussed below. However, my discussion should not be treated as representative of Dr. Amodei’s views; the project eventually broadened considerably; and my conclusions are my own. See the end of the executive summary for further acknowledgments, along with a list of experts consulted for the report.

My thanks to Nick Beckstead, Ajeya Cotra, Tom Davidson, Owain Evans, Katja Grace, Holden Karnofsky, Michael Levine, Luke Muehlhauser, Zachary Robinson, David Roodman, Carl Shulman, and Jacob Trefethen for comments on this blog post in particular; and to Eli Nathan for extensive help with the webpage.