‘Dissolving’ AI Risk – Parameter Uncertainty in AI Future Forecasting

Froolow18 Oct 2022 22:54 UTC
109 points
63 commentsEA link

1 - Summary

  • This is an entry into the Future Fund AI Worldview contest. The headline figure from this essay is that I calculate the best estimate of the risk of catastrophe due to out-of-control AGI is approximately 1.6%.

  • However, the whole point of the essay is that “means are misleading” when dealing with conditional probabilities which have uncertainty spanning multiple orders of magnitude (like AI Risk). My preferred presentation of the results is as per the diagram below, showing it is more probable than not that we live in a world where the risk of Catastrophe due to out-of-control AGI is <3%.

  • I completely understand this is a very radical claim, especially in the context of the Future Fund contest considering error bars of 7%-35% to be major updates. I will defend the analysis to a degree that I think suits such a radical claim, and of course make my model available for public scrutiny. All of my analysis is generated with this spreadsheet, which is available to download if you would like to validate any of my results.

  • Some general comments on the methods involved in this essay:

    • My approach is to apply existing methods of uncertainty analysis to the problem of AI Risk to generate new findings, which I believe is a novel approach in AI Risk but a standard approach in other disciplines with high levels of uncertainty (like cost-effectiveness modelling).

    • Rather than a breakthrough insight about AI itself, this essay makes the case that a subtle statistical issue about uncertainty analysis means low-risk worlds are more likely than previously believed. This subtle statistical issue has not been picked up previously because there are systematic weaknesses in applying formal uncertainty analysis to problems in EA /​ rationalist-adjacent spaces, and the issue is subtle enough that non-systematised intuition alone is unlikely to generate the insight.

    • The intuitive explanation for why I report such different results to everyone else is that people’s intuitions are likely to mislead them when dealing with multiple conditional probabilities – the probability of seeing a low-risk output is the probability of seeing any low-risk input when you are stacking conditional probabilities[1]. I avoid my intuitions misleading me by explicitly and systematically investigating uncertainty with a statistical model.

  • The results pass several sensitivity and validation checks, so I am confident that the mechanism I describe is real, and should affect AI funding decisions going forward. There are limitations with the exact parameterisation of the model, and I will explain and contextualise those limitations to the extent that I don’t think they fundamentally alter the conclusion that distributions matter a lot more than has previously been understood.

  • The conclusion of this essay is that for the average AI-interested individual nothing much will change; everyone was already completely aware that there was at least order-of-magnitude uncertainty in their beliefs, so this essay simply updates people towards the lower end of their existing beliefs. For funding bodies, however, I make some specific recommendations for applying these insights into actionable results:

    • We should be devoting significantly more resources to identifying whether we live in a high-risk or low-risk world. The ‘average risk’ (insofar as such a thing actually exists) is sort of academically interesting, but doesn’t help us design strategies to minimise the harm AI will actually do in this world.

    • We should be more concerned with systematic investigation of uncertainty when producing forecasts. In particular, the radical results contained in this essay only hold under quite specific structural assumptions. A considered and systematised approach to structural uncertainty would be a high-value follow up to this essay about parameter uncertainty, but would need to be written by an expert in AI Risk to move beyond surface-level insight.

    • More generally, the analysis in this essay implies a reallocation of resources away from macro-level questions like, “What is the overall risk of AI catastrophe?” and towards the microdynamics of AI Risk. For example, “What is the probability that humanity could stop an AI with access to nontrivial resources from taking over the world?” is the best early differentiator between low-risk and high-risk worlds, but it is a notably under-researched question (at least on a quantitative level)

  • Somewhat interestingly, the method used in this paper was initially developed by rationalist luminaries—Anders Sandberg, Eric Drexler and Toby Ord. Their paper is well worth a read on its own merits, and is available here.

2 - Introduction

2.1 Context

As part of the Effective Altruism Red Teaming Contest I wrote an article arguing that there were systematic limitations with uncertainty analysis within the EA space. The judges were extremely kind to highlight some of the stronger features of the article in their commentary, but they did note that I failed to adequately defend the importance of uncertainty analysis, particularly in areas in which highly sophisticated measurement and quantification are less central. While the errors of explanation were entirely mine, this article will hopefully address that gap, and function as an example of the sorts of insights that can only come from systematic application of the uncertainty analysis toolkit.

This essay focuses on parameter uncertainty, which is to say uncertainty that arises because we are unsure about numerical values for some of our inputs. There are some unique features of models of AI Risk which mean a complete and systematic investigation of parameter uncertainty leads to some very surprising and potentially important results. I will also try to complete an essay on structural uncertainty which will follow a more conventional approach and derive more conventional conclusions, which will more directly function as an example of what might be achieved with systematic analysis of uncertainty in these sorts of situations.

As a small caveat, the state of AI Risk analysis has advanced a very great deal since I was last properly immersed in it. Although I have taken steps to minimise the impact my ignorance has on the analysis (specifically by doing as much background reading as was practical in the time I had to draft the essay), it is extremely likely that I am still using terms which are a decade out of date in places. This is an essay about a statistical concept more than about any particular idea in AI Risk, so although the archaic language is probably jarring I wouldn’t expect it to lead to the sort of oversight which fundamentally alters conclusions. Nevertheless, apologies for the anachronisms!

2.2 Summary of claims

The general claim in this essay is that distribution of risk around central estimates of AI catastrophe is at least as important as the central estimates themselves. This is because most models of AI catastrophe have a number of discrete steps, all of which need to come true in order for bad outcomes to occur. This means worlds where risk is very low will be systematically overrepresented compared to worlds where risk is very high. In this essay I put an optimistic slant on this (“We probably live in a low-risk world!”), but a pessimist might argue that this mathematically means that in worlds where risk is not low then it is likely to be very high compared to what we expect.

A particularly striking demonstration of this is that the Future Fund give a 3% risk of AGI Catastrophe due to an out-of-control AGI as an example of a probability so outlandish that it would result in a major shift of direction for them; in fact, it is more probable than not that we live in a world where the risk of AGI Catastrophe of this kind is <3%.

A high-level summary of the structure of this essay is given below.

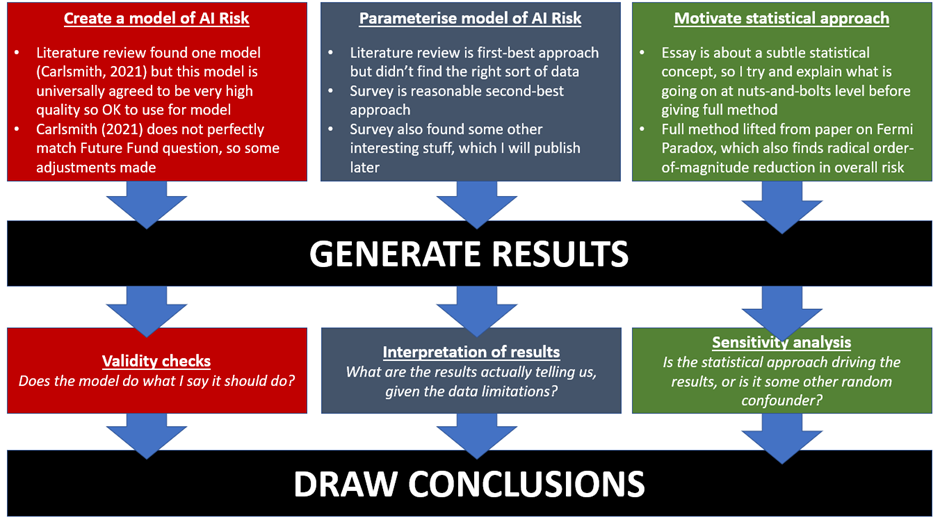
I don’t want to either oversell or undersell the claims being made in this essay. It looks only at one possible type of AI Risk (an out-of-control AGI permanently disempowering humanity), and has a number of structural and data limitations that should prompt caution before anyone makes any irrevocable decisions off the back of the analysis. On the other hand, I am quite confident the mechanism discussed in this essay is sound; if it is genuinely true that (elements of) the structure of AI Risk can be described as a series of weighted coin tosses, all of which have to come up ‘heads’ in order for this particular Catastrophe to be observed, then the conclusion is mathematically inevitable; the AI Risk community is systematically overestimating AI Risk, probably because it is extremely hard to intuitively reason about asymmetric uncertainty distribution so people are making systematic errors of intuition. Part of the length of this essay is trying to motivate an intuitive understanding of this mechanism so that even if my specific model of AI Risk is later found to be in error the core insight about distributions of risk is preserved.

It might be worth spending a moment to emphasise what this essay does not claim. A claim that we are probably living in a world where the risk of AGI Catastrophe of a certain kind is low does not mean that the risk of AGI Catastrophe is negligible. Low-probability high-impact events are still worth thinking about and preparing for, especially since the Catastrophe described in this essay is only one possible way AI could be bad for humanity. My background is health economics, so I tend to think of interventions as being cost-effective or not: most interventions to lower the risk of AGI Catastrophe that were cost-effective before this essay will remain cost-effective afterwards, since it is a good guess we are nowhere near the productivity frontier of AGI Risk mitigation given how young the discipline is. Moreover, a 1.6% chance of extremely bad AGI outcomes is actually not all that low a probability in the context of how catastrophic the disempowerment of all humanity would be. If a doctor told me a bone marrow transplant to save the life of a stranger carried a 1.6% chance of my death, then I would have to think very hard about whether I wanted to risk the procedure. Fundamentally, this essay is an argument in favour of the importance of uncertainty analysis and examining ex post distributions of uncertainty, rather than making any claims against the importance of AGI Risk.

3 - Methods

3.1 Literature review & Model Structure

Creating a model of the AI Risk decision space is not a trivial problem, and certainly not one a person with lapsed AI Risk credentials like myself was likely to get right first try. In order to identify the state-of-the-art in AI Risk decision modelling I performed a review of the EA /​ LessWrong forum archives and recorded any relevant attempt at describing the decision space. By ‘relevant’ I mean that the author explicitly laid out the logical interrelationship of the steps between now and a possible AI Catastrophe, and then assigned probabilities to those intermediate steps (in other words it was possible for me to replicate the model of the world the author had used in order to reach the same conclusions as the author). This is a significantly more restrictive filter than it might initially appear – it excludes canonical pieces of writing on AI Risk such as Yudkowsky (2008) or Bostrom (2014) because neither of these include probability estimates and it is not clear they are even supposed to be read as containing a strict logical model of the interrelationships between steps to different AI futures.

I found eleven relevant models, although this slightly overstates the findings; I found Carlsmith (2021) and then ten reviews of Carlsmith (2021) which offered their own probability estimates without offering a significantly revised model of the decision problem. I’ll refer to this conceptual map of the AI Risk decision space as the ‘Carlsmith Model’, in order to differentiate it from the specific probabilities which populate the model given in Carlsmith (2021).

The Carlsmith Model is a six-parameter deterministic decision tree which aims to estimate the probability that AI catastrophe occurs before 2070. The parameters correspond to the probability that each step on the path to catastrophe occurs, with (implicitly) all other outcomes ending up in an absorbing state that we could roughly label ‘No AI catastrophe’. In Carlsmith (2021)’s initial parameterisation, the model gives an output of approximately 5% likelihood of catastrophe. Carlsmith notes that they have later revised this estimate upwards to approximately 10%, but as far as I can see didn’t publish what changes in the intermediate parameters led to this conclusion. There is some limited uncertainty analysis around these central estimates, but this analysis was not systematic and focussed more on scenario analysis than parameter uncertainty. The model is represented in the figure below.

I validated this approach by asking the EA Forums whether they knew of any sources which I had missed, but this revealed no new quantitative models of AI Risk[2]. It did direct me to approximately twenty relevant estimates of individual steps in the Carlsmith Model – mostly in Michael Aird’s database of existential risk – which were not full specifications of the decision space themselves, but might inform individual parameters in the Carlsmith Model[3]. Overall, it makes sense to me that the Carlsmith Model would be the most appropriate model of AI Risk for this question; the framing of the question in the contest announcement specifically highlights Carlsmith (2021) as an example of best practice.

Although the Future Fund question is framed in a way that makes it clear the Carlsmith Model approach is valuable, it also distances itself from the exact probabilities given by Carlsmith (2021). In particular, the Future Fund give their central probability of catastrophe given the invention of AI as 15%, approximately three times higher than Carlsmith (2021). This is not necessarily a contradiction; Carlsmith (2021) and the Future Fund ask subtly different questions:

  • Unlike the Future Fund question, the Carlsmith Model considers the risk of catastrophe by 2070 rather than the risk of catastrophe at any point in the future after AI is invented. A number of reviewers note that this is a slightly awkward restriction on the Carlsmith Model.

  • Unlike the Future Fund question, the Carlsmith Model does not distinguish between catastrophe due to an out-of-control AI and a catastrophe due to an in-control AI being misused. This makes sense given what Carlsmith is trying to accomplish, but is a limitation given what the Future Fund are trying to accomplish (specifically, the two outcomes suggest radically different strategies for funding decisions)

  • The Carlsmith Model is not conditional on AI being invented by 2070 (i.e. there is a step in the Carlsmith Model which is abstracted away in the Future Fund contest), so even if they agreed completely the Future Fund would estimate a higher probability of catastrophe, because AI is sometimes not invented in the Carlsmith Model.

Since this essay considers the Future Fund question explicitly (rather than a repeat analysis of Carlsmith), the specific parameterisation of Carlsmith (2021) was not appropriate, and primary data collection was required to parameterise the model.

3.2 Model Parameterisation

Due to the above limitations of applying the parameters of Carlsmith and his reviewers directly to the Future Fund question, I surveyed the AGI Risk Community[4] with this instrument, which asks exactly the correct questions to match the Future Fund’s question to the structure of the Carlsmith Model. In particular, note that the instrument does not condition on the catastrophe occurring by 2070, and also includes an explicit differentiator between catastrophe due to an in-control AI and an out-of-control AI. I am not a triallist and have no particular expertise in survey design beyond hobbyist projects, so in hindsight there are some design errors with the survey. To this end I would normally suggest that an expert replication of the survey would be valuable, except I think the MTAIR project will be so much better than what I have done here that a replication would be a waste of resources; it is reasonable to use my numbers for now, until MTAIR gives a ‘definitive’ view on what the correct numbers should be. However, it is also prudent to be aware of the limitations with my numbers until MTAIR reports—the biggest weaknesses that I have identified are:

  • The most major omission was not explicitly conditioning all estimates on the possibility of catastrophic existential risk. Some respondents did condition their estimates on this, some respondents assumed I implicitly meant ‘conditional on no other existential risk occurring…’. This is not the end of the world[5] because it can be routed around with good structural uncertainty analysis, but on average responses will be slightly too high.

  • There was ambiguity in some of the questions. For example, one question asked about ‘Alignment’ and it was clear some respondents had differing ideas about what that meant in practice. Someone more expert on AI than me wouldn’t have made those errors, and could probably have identified a better set of questions to ask than just covering a summary survey of Carlsmith (2021).

  • I didn’t offer an opportunity to specify a distribution when respondents gave their answers. This was a deliberate omission because I was going to generate the distributions myself with the SDO method I describe below. However, some respondents described how they had quite complex responses (e.g. bimodal responses) and couldn’t give genuinely accurate answers without the ability to specify distributions of uncertainty.

  • The survey doesn’t force people to assume AI is invented before 2070, which the Future Fund would like you to assume. This affects seven responses which estimate AI will come later than 2070, plus three more which estimate AI will be invented in 2070 exactly. In theory this could have affected responses because people’s risk estimates could be correlated – for example AI being invented in 2500 gives more time for other sources of x-risk to cause a catastrophe. In practice there wasn’t a significant difference between pre-2070 and post-2070 responders so I have included all responses together.

42 people took the survey. Of these, 14 self-identified as experts—either fully or marginally—and I have separated out responses from these individuals as a separate subgroup in the results.

Generally, data quality was good. The most major issues with data quality was inconsistency with how percentage values were entered (“50%” vs “50″ vs “0.5”). A validation question at the end ensured that all of these errors were caught and corrected. Similarly, some individuals wrote short explanations of their estimates in the response box itself rather than the comment box, but these were also easy to detect and resolve. One rather lovely thing about rationalist-adjacent communities is that when people fill out a survey with odd data they are self-aware enough to recognise the issue and kind enough to explain exactly what their thought process was leading to it. So, for example, when I asked for the year people thought AGI would be invented and someone put a date in the past, they very helpfully explained that they knew this would normally be rejected as junk data but in this particular case they really did mean they thought it already existed!

With this in mind, only very minor data cleaning was undertaken. Aside from normalising probabilities and removing explanatory text, the only data adjustment was a slight compensation for entirely certain estimates. Specifically, any estimate which gave probabilities of 100% or 0% was adjusted to 99% and 1% respectively. This had to be performed in order to allow the conversion of probabilities to odds, and was justified on the basis that entries of 100% or 0% must have been intended as a shorthand for ‘almost completely certain’ rather than actually expressing complete certainty[6]. No other result was adjusted, which means that a reported probability of 99.9% ended up being more certain than a reported probability of 100% in the final analysis. That is slightly inelegant, but it won’t materially affect results generated with the SDO method described in the next section. It might slightly alter some summary statistics generated without the SDO method, but since the whole point of this essay is that those summary statistics are misleading I haven’t added any correction or validation around this point.

Summary results of the survey are reported below. I will update this sentence with a link to the full results dataset once I have had a chance to anonymise them properly[7].

In general, these responses are consistent with the Future Fund’s position on the risk of AI Catastrophe, in the sense that all approaches give a number which is in the 10%-50%-ish order of magnitude. The responses are generally slightly higher than the Future Fund estimate, and I’m not sure why that is – it could be that the Future Fund is unusually conservative on AI Risk by community standards, or it could be a bias I accidentally embedded into the survey and have not identified. Experts are more worried about AI than non-experts, but this seems easily explainable by a selection bias (only people who think AI is very worrying would invest the time and resources to become expert on it).

People’s responses are quite internally valid – their overall estimate of the risk of AI Catastrophe is roughly the same as the estimate made by multiplying each individual step in the sequence together. Furthermore, the agreement between the Expert and the Full dataset is overall good on specific questions. The only exception to this is that there is a substantial difference between the Expert and Non-Expert view of AGI scaling – that is, the probability that an AGI that is given an initial endowment of some high-power resource will convert that endowment into something that can subjugate all of humanity. Non-experts give roughly even odds that we will be able to ‘correct’ a misbehaving AI, whereas Experts suggest that 3 times in 4 we will not be able to fight /​ contain /​ bargain with a misbehaving AI. This is the only major difference between the two groups, and appears to drive almost all of the difference in overall result between the Full and Expert dataset.

As a point of analysis, one interpretation of this is that what makes people worried about AGI is fear that we cannot contain a Misaligned AI. That is (pending confirmation of the result) the most effective way for Experts to evangelise AGI Risk would be taking people who are complacent about our ability to contain a Misaligned AI and convincing them it would actually be 1-in-4 hard rather than 1-in-2 hard. A sketch model of the problem space is that non-worriers think of AI deployment as being a bit like virus research – for sure governments are going to do it, for sure someone is going to do something stupid and unleash a pandemic on the world, but probably someone will invent a vaccine or something and everything will be fine. There’s no point trying to convince Non-Experts that Alignment will be tricky because they already agree with you!

Overall, my view is that the Full Survey Dataset is probably more reasonable as a base case than the Expert Survey Dataset. There isn’t really any objective definition of ‘expert’ that would mean that we have any reason to trust the Expert Survey Dataset more, and the Full Survey Dataset gives a response which is closer to what the Future Fund says is its central estimate, making it more appropriate for this particular application. My main reason for including the ‘Expert’ filter was in case Non-Experts gave completely invalid /​ inexplicable answers, but this did not actually happen – the demographics of the AI Risk Community obviously skew more conscientious than the general population.

Finally, I include a brute-force sense check on my survey work – as a sensitivity analysis I simply multiplied the implied odds given by Carlsmith (2021) and his reviewers by 1.5 and set the ‘probability AGI invented’ parameter to 100% with no uncertainty. This gives the same overall risk of catastrophe as the Future Fund, and so might be in approximately the ballpark of the figures we would get if we asked Carlsmith and their reviewers to repeat the exercise again with precisely the question Future Fund was asking. To be clear, this is a completely ad hoc step with no methodological justification: if Carlsmith intended for any of his estimates to be correlated, I have just broken this correlation. If he had better evidence for some parameters than others I have just deleted this evidence. And so on.

Many thanks to the 42 respondents who have made the forthcoming analysis possible by sharing their expertise and insight.

3.3 Statistical methods

3.3.1 Motivation

As described in the introduction, the statistical methods used in this essay have an interesting heritage. I am lifting the method entirely from Sandberg, Drexler and Ord (2018) – hereafter ‘SDO’ - and these three authors are all rationalist-adjacent in different ways. As far as I know they are all actively interested in AI Risk, so I am a little surprised that they have not applied their method to the problem described in this essay. My guess is that they are too professional to rely on pure survey data as I have done and without this survey there is currently not enough data to use their method.

SDO’s insight was that for a certain class of problem it is extremely dangerous to implicitly treat parameter uncertainty as not existing. They demonstrate this by ‘dissolving’ the Fermi Paradox. The Fermi Paradox is the strange contradiction between the fact that reasonable estimates for the number of intelligent civilisations in the universe who should be trying to contact us put the number very high, but when we actually observe the universe we do not see any signs of intelligent life other than our own. SDO’s argument is that all prior investigations have treated parameter uncertainty as though it doesn’t exist, and as a result tried to calculate the number of alien civilisations we should see. However, SDO argue that this is an incorrect framing; what we are interested in is the probability we see any alien civilisations at all.

This is confusing, and I don’t think trying to pretend otherwise is helpful. Surely, you might think, a high number of alien civilisations (on average) should translate to a high probability of being contacted by an alien civilisation? What made it ‘click’ for me was rereading a comment by Scott Alexander on this study:

Imagine we knew God flipped a coin. If it came up heads, He made 10 billion alien civilization. If it came up tails, He made none besides Earth. Using our one parameter [equation], we determine that on average there should be 5 billion alien civilizations. Since we see zero, that’s quite the paradox, isn’t it?

No. In this case the mean is meaningless. It’s not at all surprising that we see zero alien civilizations, it just means the coin must have landed tails.

I wouldn’t expect to be able to communicate statistics better than Scott Alexander, but I’ve included a second possible construction of this point (my own, this time) in case a different perspective helps explain the issue:

You work in retail. A survey shows you that the average human has less than two legs (because some people have one leg, or no legs). You order all your trousers to be lopsided to account for the fact that a trouser with 1.97 legs matches the average human best. You are surprised when none of your trousers sell. The average number of legs per human matters less than the distribution of those legs.

Part of the reason this is unintuitive is that for most probability problems we come across in everyday life, the number /​ probability distinction is basically irrelevant. If we throw a large number of dice onto a table then the number of sixes we see relative to other numbers is a pretty good proxy for the probability that we see a six on the next roll. So, most problems are not going to ‘dissolve’ in the way SDO make the Fermi Paradox behave. The specific features of the Fermi Paradox that make it very suitable for the SDO method are:

  1. We reach a final estimate by multiplying conditional probabilities together (ie probabilities for events that depend on whether earlier events in a chain of logic come to pass or not)

  2. We are uncertain about those probabilities, often to the extent that our uncertainty spans several orders of magnitude

  3. There is an enormous, disjunctive, difference between one possible outcome and all other possible outcomes

AI Risk clearly meets points 2 and 3 (although our uncertainly probably spans fewer orders of magnitude than for some parameters in the Fermi Paradox) and my literature review suggested that the most generally accepted model of AI Risk meets point 1. Therefore, we might expect AI Risk to ‘dissolve’ in a similar way to the Fermi Paradox. What we need to prove this is a method for systematising this observation.

3.3.2 Synthetic point estimates

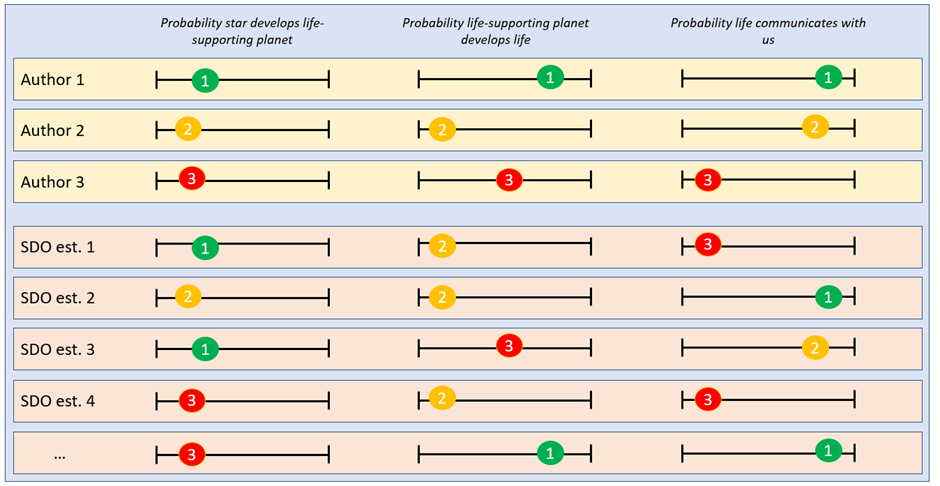
The method used in SDO to make the Fermi Paradox ‘dissolve’ is described as ‘synthetic point estimates’. The authors review the literature on the Fermi Paradox, and extract any estimate of any parameter which makes up their equivalent of the Carlsmith Model (the ‘Drake Equation’). They then populate a ‘synthetic’ Equation of their own by randomly picking one estimate per parameter. They do this many times to form a “collective view of the research community’s uncertainty”. The diagram below might help illustrate this process.

It might be helpful thinking about what the SDO method is going to show in sketch terms before letting it loose on the Full Survey Dataset – this might help motivate the intuition behind the rather startling headline results. Let’s look at the distribution the SDO method would find for one particularly interesting question, “Conditional on [being exposed to high-impact inputs] what is the probability AGI will scale (in aggregate) to the point of permanently disempowering roughly all of humanity?”. The graph below shows every survey response to this question in orange blobs (obviously including some overlapping responses). The blue line was my attempt to create a smooth distribution through these points, to help show where there are overlapping points better [8].

Imagine for the sake of argument that the Carlsmith Model was just this distribution of points repeated six times. The most likely outcome of sampling randomly from the pool of possible answers to the question is 60%, so we might very roughly imagine that the output of the toy-Carlsmith model would 60% six times in a row for a toy-probability of AI Catastrophe of about 5%. The distribution of points is very roughly symmetric, so we’d expect that for every time the model sampled high (70%, say) it would likely sample an equivalent low score a few draws later (50%, say) and so the uncertainty would cancel itself out (we might expect) – 60% * 60% * 60% is very roughly the same number as 50% * 60% * 70% so there is some empirical basis for making this assumption (we might incorrectly conclude). Doing this sampling process just six times isn’t really enough time for central limit theorem to assert itself and so we couldn’t say with confidence that every high draw would certainly be cancelled out, but on average and for practical applications we could be reasonably confident that high and low draws are equally likely.

To be clear, this chain of logic is incorrect – however it is implicitly the chain of logic followed by every single structural model of AI Risk I came across during the literature review, including many discussions where explicit probabilities weren’t given but it was clear that the author had this sort of structure in mind.

In the diagram below I have colour-coded the diagram above to make this point. The red area are draws which are low enough that they make a difference to the overall result (<10%), the orangey-yellow area are draws middling enough that they don’t really affect the final result on expectation and the green area are draws high enough that we might expect them to cancel out the draws in the low area (>90%)

The ‘trick’ here is that the high and low draws do not cancel each other out. In the diagram above, a single draw in the red area functionally means the final probability will be much less than 5%. Imagine for example a scenario where four down-the-middle 60% draws were made, and then a draw of 10%. The overall probability would be 60%* 60%* 60%* 60%* 10% = roughly 1%. So already the probability of the event after five samples is less than our naively anticipated probability after six samples! You might object that this is unfair and that I have just selected a low draw with no compensating high draw. So, let’s assume our final draw is a perfect 100% probability on the final parameter of the toy-Carlsmith model. That means we take our slightly less than 1%, multiply it by 100%… and of course it doesn’t go upwards at all; 100% of any probability is just the probability you started with!

For me, this is the absolutely critical mechanic to understand in order to grok what is about to happen to convert a naïve 18.7% estimate of risk from the survey with with no uncertainty into a synthesised 1.6% chance of risk with parameter uncertainty – intuitively we think of conditional probabilities as being like numbers, but they don’t actually act like numbers in all situations. If the graph above represented my productivity at the widget-factory each day then a bad day (red area) on Monday genuinely could be offset with a good day (green area) on Tuesday. However, because these are conditional probabilities, a bad day on Monday starts me off in a worse position on Tuesday – the best I can do is try to hang on to my already low endowment.

So conceptually, what we are really interested in with the synthetic point estimate is not so much the central estimate for the probability of continuing on to the next step, but rather the distribution of estimates within each parameter (you might notice a bit of a recurring theme here…) Specifically, we are interested in the probability that any particular parameter is sampled low enough that it completely throws off all subsequent calculations. This is significantly more likely to occur when estimates span multiple orders of magnitude, and this is why the SDO method is particularly suitable for some applications (Fermi Paradox, AI Risk) and no better than a simple average in some other applications (rolling dice, predicting sports team victories)

4 - Results

4.1 Base case

4.1.1 Main results

The main results are based on 5000 simulations of the Full Survey dataset, using the Synthetic Point Estimate method from SDO. The outputs of the base case are displayed below. The panel in the top left represents the probability that we live in a world with one of a number of different ‘categories’ of risk, and the panel in the top right offers summary statistics of this graph. The interpretation of the line graph at the bottom is slightly fiddly; the area under the curve between a 0% probability of catastrophe and x% probability of catastrophe represents the fraction of possible worlds with a less than x% risk. Please also note the log scale.

The ‘headline’ result from this analysis is that the geometric mean of all synthetic forecasts of the future is that the Community’s current best guess for the risk of AI catastrophe due to an out-of-control AGI is around 1.6%. You could argue the toss about whether this means that the most reliable ‘fair betting odds’ are 1.6% or not (Future Fund are slightly unclear about whether they’d bet on simple mean, median etc and both of these figures are higher than the geometric mean of odds[9]). However, the whole point of this essay is to encourage people to move beyond summary statistics and do systematic uncertainty analysis, so I don’t want to over-emphasise the 1.6% figure.

In reality, the most important feature of this analysis is the panel in the top left, showing a very high probability that the world we actually live in has a very low risk of AI Catastrophe due to an out-of-control AGI. About 38% of all simulations fall into this category, and another 13% or so before the risk reaches 3%. I think the best conclusion of the Survey dataset is that it is most likely that we live in a world where AI Risk is very low (<3%). This accurately captures and characterises the distribution of possible worlds we might experience, and I think also helps make the ‘so what’ of the analysis more concrete.

A clear implication of this is that there are some worlds where the risk of catastrophe must be absolutely terrifying, to balance out this probability mass of low-risk worlds so that end up with a simple average probability close to the Future Fund’s central estimate. In fact, this is what we see – around 5% of the probability mass covers worlds where the risk of out-of-control AI catastrophe is 50% or greater (i.e. we are as likely to be catastrophically disempowered by an AGI via this one single mechanism as not). Each of these ‘high risk’ worlds cancels out a large number of ‘low risk’ worlds unless you statistically correct for that effect, which one reason why the simple mean ends up so much higher than the geometric mean of odds. So whereas I have placed an optimistic slant on the results (“It is highly likely we live in a world where AI Risk is low”), a pessimist might say, “…but on learning we don’t live in a low-risk world, we also learn that AI Risk is much, much higher than we expected before”.

Please also note that my computer stubbornly refuses to calculate the true geometric mean of odds of the distribution by taking the 5000th root of the results, so I’ve used an approximation. However, this approximation is close enough to the actual value that you can treat it as being correct for the purpose of discussion.

4.1.2 Interpretation

One important question we might therefore want to ask is, “Do we actually live in one of the 50% of low-risk worlds? Or do we actually live in one of the one of the worlds where the risk of AI Catastrophe is worse than the Future Fund estimate?”

This is actually a remarkably difficult question to answer – I answered an analogous question as part of my PhD and it took me deep into machine learning territory I never want to revisit. There are some fairly robust statistical approximations we can use, and even better there are some nice visualisations answering the same question. The graphs below display probability density functions for each question asked in the Carlsmith Model. The density function for ‘safe’ worlds (risk <3%) is graphed in green, the density function for ‘dangerous’ worlds (risk >35%) is graphed in red. What we are looking for is a different shape between the green and red lines that we could use to infer a difference between ‘safe’ and ‘dangerous’ worlds – so for example “There will be strong incentives to build APS systems” is not very interesting to us because the lines basically overlap, but “Alignment is hard” is potentially interesting because there is a big probability mass on the left of the ‘safe’ graph which does not exist in the ‘dangerous’ graph. What this means is that if we can refine our understanding of whether “Alignment is hard” to be confident it is at or below 20%, we can be fairly confident we live in a ‘safe’ world – almost no ‘dangerous’ worlds have a low risk that “Alignment is hard” and very many ‘safe’ worlds do.

StatementDistribution
There will be strong incentives to build APS systems
Alignment is hard
The AGI system will NOT be deliberately tasked with actions which result in the extinction of humanity
Some deployed APS systems will be exposed to inputs where they seek power in misaligned and high-impact ways
Some of this misaligned power-seeking will scale (in aggregate) to the point of permanently disempowering ~all of humanity
This will constitute an existential catastrophe

It is horrifically easy to misinterpret these graphs just by eyeballing them, because – at the very least – the base rate of ‘safe’ and ‘unsafe’ worlds is different so you need to use a Bayesian framework to make actual probability judgements. However, there are also a few quite useful implications here if you are prepared to use such a framework. In particular, the highest value of information of AI Risk microdynamics is establishing whether the probability that AI will be deliberately tasked with ending humanity is less than about 60% and whether the AI will scale in power to the point of disempowering most of humanity is less than about 50%. These are the probability judgements that add the most information about whether we live in a ‘safe’ or ‘dangerous’ world. Since the first of these scenarios involves an AI killing most of us anyway (it just isn’t ‘out of control’), realistically the second case is the one we are most interested in.

That is to say, to a first approximation we will learn more about whether AI is likely to lead to existential catastrophe by asking specifically about Containment scenarios than by asking about any other single element of the Carlsmith Model. This is potentially highly actionable for funders, as I don’t think this information was previously known.

4.2 Sensitivity Analysis

‘Sensitivity analysis’ is the process of ensuring that I haven’t just cherry-picked data to get the result I wanted. There are two pre-defined sensitivity analyses I described in the text above. The first is an ‘Expert Only’ subgroup of the Survey Data, the second is a Modified Carlsmith version of Carlsmith (2021) and his reviewers. These outcomes are reported below:

4.2.1 Expert only subgroup

4.2.2 Modified Carlsmith

4.2.3 Interpretation

Both sensitivity analyses show the same basic pattern as the main analysis; the simple mean of results is roughly in line with the Future Fund estimate, but that ‘the mean is misleading’ and the distribution of results disproportionately favours very low-risk worlds. Whereas around half of all possible worlds are very low risk (<3% risk) in the base case, only around 35%-40% of possible worlds are very low risk in the two sensitivity analysis cases. The ‘Expert Only’ analysis shows the flattest distribution of the three analyses conducted so far, and hence has the highest geometric mean of odds. The ‘Adjusted Carlsmith’ analysis has a slightly higher median but a sharper distribution and hence a geometric mean of odds somewhere between the base case and ‘Expert Only’ case.

It is common in analyses of these sorts to go back and retroactively pretend that Modified Carlsmith was supposed to be the main result all along, and put the two Survey analyses as sensitivity. This means that you can say, “My sensitivity analysis gave me results a bit above and a bit below my main analysis, so I’m confident I’ve triangulated the risk correctly”. I don’t think that would be intellectually honest in this case; notwithstanding that I pre-committed to using the Full Survey results before I knew the outcomes anyway, the Modified Carlsmith has no theoretical basis for use (it is inappropriate to just multiply odds by 1.5x to get at what the authors ‘would have reported’ if asked a completely different question). Overall, I am satisfied that the sensitivity analysis supports the main argument of this essay, which is that uncertainty analysis around the distribution of risk in AI Futures is more important than has been acknowledged to this point. I am also satisfied that the sensitivity analysis supports a view that the best estimate for a community consensus on the risk of AGI incorporating uncertainty is somewhere around or below the 3% threshold Future Fund specify would be a ‘major’ change.

4.3 Validity Checks

‘Validity checking’ is the process of ensuring that the model actually outputs what we expect it to output. The gold standard here is to have someone double-check my work cell-by-cell (and I would invite you to download my model and do so from this link). However more commonly we would conduct analyses with particular features in order to ensure the output behaves in the way we expect it to – for example setting values to zero and making sure the output is zero and so on. In this section I’ve highlighted three such analyses which I think give an interesting perspective on the results.

4.3.1 Unadjusted Carlsmith

A very simple validity check is to run the SDO method on the unadjusted data generated by Carlsmith and his reviewers. Since we know Carlsmith (2021) is amongst the best-regarded and best-validated models of AI Risk in the AI Risk Community, this validation check completely abstracts away all the imperfect data collection decisions I have made. This isn’t a good check on the Future Fund question specifically, but rather the claim that before 2070 we would expect to see an AI Catastrophe from any source (not just an out-of-control AGI). The results are basically where we would expect them to be – the probability of being in a low-risk world is much higher than the probability of being in a high-risk world.

4.3.2 ‘Negative Validity Check’

A second validity check is ensuring that the SDO method doesn’t produce these skewed distributions when the SDO assumptions don’t hold (i.e., did I get my implementation of the maths right?). My claim in this essay is that we don’t intuitively understand uncertainty analysis of conditional probabilities, and acting as though uncertain conditional probabilities are certain leads to error. If I generate the same ‘error’ with data where our intuition should be reliable, it implies a problem with the SDO method rather than our intuition. The simplest SDO assumption to relax is that we have significant uncertainty about our parameters, which is also the central claim in this essay and so a negative result here would fundamentally upend the rest of the analysis. In the validity check below, I use the (unadjusted) Carlsmith (2021) estimates, and randomly ‘perturb’ each parameter 20 times to a maximum deviation of 1% from the original estimate. I then perform the SDO method as described above. The result is below. It shows almost exactly the same thing as the Carlsmith point estimates, which is exactly as expected (remember that the original Carlsmith (2021) paper includes a term for whether AI is actually ever invented, whereas this is abstracted out of all analysis conducted for the Future Fund). The only reason the graph appears to have any uncertainty at all is that I do some smoothing to the final curves.

4.3.3 (Very basic) Structural uncertainty analysis

The final validity check I thought might be interesting was to demonstrate how sensitive the results were to structural sensitivity. For example, an unsophisticated objection to the SDO method is that you could use it to generate arbitrarily low probabilities by adding increasingly arcane parameters to the model about which we are uncertain (“…and the universe still exists due to false vacuum collapse” etc). The most sophisticated critique of the SDO method along these lines is probably here – the author argues that, for example, life might arise in places other than planets, so the structure of the Drake Equation shouldn’t have a term for ‘Mean number of planets that could support life per star with planets’ because it overfits the model. With respect to the more sophisticated version of the critique of SDO, we might imagine that some terms in the Carlsmith Model are redundant however carefully Carlsmith workshopped his paper. For example, maybe we think that an AGI disempowering humanity and bad outcomes for humanity are so inextricably linked that we shouldn’t separately sample from them. Similarly, perhaps we think that deploying an AGI on any real-world application whatsoever automatically means the AGI can escape confinement and gain access to high-impact resources. We could therefore create a ‘truncated Carlsmith model’ to take account of this.

The results of the Truncated Carlsmith Model validity check are below. Overall, there is some evidence that the probability of living in a very low-risk world is smaller in the Truncated Carlsmith model (although the geometric mean of odds is largely unaffected). In general, this makes sense to me – the fact it is now impossible to make six ‘low’ draws in a row rules out the possibility of the ridiculously low 10^-6-level probabilities we see in the base case model, but it doesn’t fundamentally alter the fact that a single low draw on any of the four remaining parameters puts us at or near a ‘low risk’ world. Furthermore, the probability of making a low draw increases in both of the grouped parameters, since anyone who had a low value for one and a high value for the other now has a low overall value as a mathematical consequence of multiplying probabilities.

4.3.4 Interpretation

The reason I selected these validity checks is because these three validity checks together imply:

  • The use of a survey isn’t the thing driving the results – there might be weaknesses with the survey, but the central insight that uncertainty analysis is neglected would survive a major weakness being discovered in the survey.

  • The use of the SDO method isn’t creating the results out of nothing – SDO only creates striking results when uncertainty around parameters is neglected

  • The specifics of the Carlsmith Model isn’t multiplying uncertainty unnecessarily – although there is certainly structural uncertainty analysis which should be performed (and I will try and perform it in a later essay), this relates more to the general concept of multiplying conditional probabilities together to arrive at an overall risk. If you merely want to tinker around with the specifics of the Carlsmith Model you will arrive at a very similar result to the base case.

These three points are the major pillars I expect objections to this essay are likely to attack. The reason I think this validity analysis is helpful is that even if one of these pillars collapses the general thrust of my conclusion remains. For example, I personally think the weakest element of the argument is the implicit premise that a survey of the AI Risk Community is the same thing as generating a reliable distribution of AI Risk probabilities. Let us suppose I am wrong about this and in fact the only reliable way to generate accurate beliefs around AI Risk is careful expert review of longform essays about claims, which I cannot do as I don’t have the social capital to get AI experts to produce such data. Nevertheless, I can be confident that my general conclusion would remain if I undertook this process; because the mechanism of SDO isn’t specific to any particular dataset (provided there is order-of-magnitude uncertainty on some parameters), I can be confident that those experts would have intuitions that would mislead them and the SDO process would produce this striking result.

5 - Analysis

5.1 Strengths and weaknesses of analysis

The purpose of this essay is to argue that uncertainty analysis has been systematically neglected by rationalist-adjacent communities with an interest in forecasting the future. Consider that prior to this essay, the gold standard analysis of systematic uncertainty in AI Risk prediction was from Carlsmith (2021) and looked like the below:

I don’t intend this as a slight on Carlsmith (2021) at all – the only reason this essay is even possible is because Carlsmith performed an incredible piece of work in making explicit structural claims about AI Risk. I think I have something to add on the topic of systematic investigation of uncertainty, but his non-systematic coverage of this topic is light-years ahead of anything I could have produced. Moreover, SDO’s insight is not at all obvious – people have been theorising about the Fermi Paradox for years before SDO ‘dissolved’ it, and nobody else hit on the idea that the solution might have been contained within the uncertainty analysis, rather than uncertainty analysis being something you grudgingly do prior to publication.

There are therefore some elements of the analysis I am quite proud of – in particular I think it sets a new benchmark for appropriate parameter uncertainty analysis in AI Risk spaces. I am really pleased to make a contribution in this area, however minor it is.

However, there are elements of the analysis which are not so good. The main weaknesses of the analysis are:

  • I am relying heavily on survey data being representative of the underlying reality of the world. That is, my headline result is actually that the AI-interested rationalists believe there is a 1.6% risk of catastrophe once you have correctly adjusted for asymmetric distributions of risk. To the extent you believe the ‘wisdom of crowds’ applies to AI forecasting this is not a problem, but to the extent you think that rationalists will systematically over- or under- estimate AI risk my results will be wrong to the same degree.

  • The SDO method is incredibly brittle to correlated parameters. If, for example, the probability that AI is invented is correlated with the probability that Alignment is easy (for example because whole-brain emulation turns out to be the best path to AGI and Alignment is easy when you’re literally simulating human values) then the SDO method doesn’t work – it can’t randomly sample from the Alignment question, because it needs to weight its sampling based on what it picked in the Invented question. I did some initial experiments into whether this was possible to fix by converting the synthetic point estimate to a synthetic distribution estimate, and my conclusion is that this objection isn’t fatal but it needs a better statistician than me to get it implemented.

  • A review of the literature uncovered only one structural model of AI Risk to inform usage of the SDO method. Structural sensitivity analysis is therefore very limited. For example, one significant structural assumption is that this model assumes only one AGI is ever invented. That is, I think everyone is implicitly always talking about the AGI that comes closest to causing a catastrophe for humans in every possible world when they are forecasting probabilities. However, if successfully containing one AGI doesn’t mean you’ve successfully contained the next AGI then the Carlsmith Model greatly misspecifies the AGI landscape. I will attempt to write a second (mercifully shorter) essay with a method to address this, but it is too much to include in one place so it is a limitation of the analysis here.

5.2 Implications of analysis

5.2.1 Implications for individuals

If my analysis is correct, then there is a high probability that we live in a world where the risk of AI Catastrophe due to out-of-control AGI is significantly lower than (most of) the AI Risk community initially believed. I don’t think my position is especially iconoclastic – “shut up and multiply” is a fairly common saying in rationalist-adjacent spaces for a reason – but I accept for some people it could trigger a re-evaluation of their existing beliefs. If we do live in such a world, does this imply a radical restructuring of anyone’s beliefs? I think probably not for individuals, for three reasons:

  1. The most extreme analysis of my data you could imagine would still be within an order of magnitude of basically all community consensuses, including the Future Fund estimate. There are very many AI-related questions and forecasts over which we have significantly worse than order-of-magnitude accuracy, so this analysis should be understood as being wholly consistent with the existing AI paradigm (note that that is quite different to SDO’s application in the Fermi Paradox space, where their method totally blew all existing analysis out of the water). If you were comfortable with order-of-magnitude imprecision before you should be comfortable with it now, even though the central estimate has shifted within that order of magnitude.

  2. In general, the probability of AI catastrophe due to out-of-control AGI is not as relevant as the expected value of preventing AI catastrophe through this route, for example expressed as the value of future QALYs not accrued because of that catastrophe. More specifically – since I am an economist – I’d suggest the most relevant framework for considering the problem is the cost-effectiveness of interventions designed to lower AI risk. On that framework it sort of doesn’t matter whether the risk of catastrophe is 1% or 10% or 100% - there’s a lot of stuff we could be doing cost-effectively at the moment that we are not, and we can perhaps worry about things on the 1% vs 10% margin when we’ve completely saturated the low-cost high-impact interventions with money.

  3. This only considers one particular model of AI Risk – one where an out-of-control AI permanently disempowers humanity in a bad way. There are very many other scenarios in which AI could be bad for humanity, for example scenarios where one country uses an AI to wage a genocidal war against other countries. There are also scenarios where being overcautious regarding AI is bad for humanity, for example scenarios where AI research is deliberately slowed down because of concerns over risk and then a pandemic wipes out all life on earth because we didn’t have access to an AI to develop a cure. What I mean to say by this is that this essay is not (and is not intended to be) the final word on uncertainty analysis in AI Risk, so radically updating your belief should be conditional on more analyses like this being published to cover other AI Risk scenarios.

5.2.2 Implications for funding bodies

However, for organisations /​ fundholders this analysis might potentially prompt some thought about the best way to distribute resources. Some high-level implications of my analysis are:

  • Strategies for preventing AI Risk should start from the premise that there is a good chance we live in a low-risk world:

    • Instead of preparing for a middling-ish risk of AGI Catastrophe due to the risk of out-of-control AGI, we should be preparing (at least) two strategies for the possibility that we live in one of a high-risk or low-risk world, and plan accordingly. For example, in a high-risk world we might be prepared to trade away a lot of the potential economic advantages of AGI in order to prevent it disempowering humanity, whereas in a low-risk world we might treat AGI Risk like we currently treat natural pandemic risk (that is, mostly the honour system, followed by a massive commitment of resources if a pandemic breaks out).

    • To this end, we should be devoting significantly more resources to identifying whether we live in a high-risk or low-risk world. The ‘value of information’ here is potentially trillions of dollars of AGI resilience infrastructure we do not need to build.

  • Risk microdynamics are extremely understudied. For example:

    • It seems like there is a difference between Expert and Non-Expert predictions of overall AI Catastrophe which is driven almost entirely by different beliefs about how easy it will be to Contain an AI which is trying to disempower humanity. When funding outreach /​ explanations of AI Risk, it seems likely it would be more convincing to focus on why this step would be hard than to focus on e.g. the probability that AI will be invented this century (which mostly Non-Experts don’t disagree with). Are there more dynamics like this that could improve outreach?

    • It is clear some steps between AGI being invented and AGI catastrophe are more uncertain than others, and this is driving the broad distribution of results we see. If we were more certain about the most uncertain steps in the process then this would have a disproportionate impact on our certainty over what kind of world we live in, and therefore our response to the sort of future we were likely to experience. A good candidate for this sort of investigation is the probability that we can ‘Contain’ an AI attempting to disempower humanity. If we can do this with ~60% probability or better, it is very likely we live in a ‘safe’ world.

    • More generally, I’d imagine that the Carlsmith Model is also not the last word in structural analysis of possible AI futures. How different structural specifications of risk affect overall risk is not well understood in the AI space, and future commissioned research could (and probably should) seek to resolve this issue. This is by far the most important gap in understanding suggested by this essay, but also the one that looks most set to be quickly filled, thanks to the MTAIR project.

  • SDO’s method is not so complex that an intelligent layperson couldn’t have spotted the problem given access to the Survey Data I generated (my main contribution was knowing to look for a problem in exactly that spot in the first place) However, community norms in AGI spaces do not reward systematic investigation of uncertainty, and few people actually enjoy undertaking analysis of uncertainty just for the sheer thrill of it. It is really good that Carlsmith’s work is getting such a lot of praise, because it takes the AI Risk Community in a direction where major statistical issues like that described in this essay are more likely to be spotted early. Funders may want to consider accelerating this direction of travel, and commissioning many more systematic investigations of elements of uncertainty, using different elements of the uncertainty analysis toolkit. Funders might also want to reward /​ commission work that would form the building blocks of such analysis, such as Michael Aird’s database of existential risk.

6 - Conclusions

This essay makes an extremely striking claim; analysis of uncertainty reveals that the actual risk of AI Catastrophe due to out-of-control AGI is almost an order of magnitude less than most experts think it is. To the extent that I even dare make such a bold claim, it is because of the strong community norms to take weird results seriously, especially if they expose a failure mode in intuitive reasoning. At least part of the purpose of the essay is to make the case that we shouldn’t spend so much time focussing on single estimates of AI Catastrophe, and should instead consider distributions of results. To that end I would say that the main result I want to communicate is that it is more probable than not that we live in a world where the risk of AGI Catastrophe due to out-of-control AGI is <3%.

This is still an extremely striking claim, but one that is slightly more consistent with existing beliefs about AGI Risk – a large number of low-risk worlds are balanced out by a small number of high-risk worlds, such that when you take a simple average of risk you end up with a middling-ish number (perhaps around 15%), but when you consider the asymmetric distribution of high- and low-risk worlds you end up with a much lower number.

In this essay I propose a mechanism for why AI Risk analysts might have persisted with the belief that the distribution of uncertainty was symmetric. In my experience, people are not inherently comfortable reasoning about probabilities in their head – for example, people intuitively feel like if a chain of reasoning has a lot of high probabilities and a single low probability that the outcome must surely have at least a middling probability, when in fact the overall outcome will (on reflection) clearly be lower than the lowest probability in the chain of logic. People are also uncomfortable reasoning about uncertainty, especially when the distribution of uncertainty isn’t a nice symmetric normal or uniform distribution. When distribution of uncertainty is more or less symmetric is can be abstracted away for most purposes, but this mental habit gets people into trouble when the distribution is asymmetric. Given these two hypotheses, it stands to reason that people would be extremely uncomfortable reasoning about uncertain probabilities, which, unfortunately, is exactly what is required to make accurate forecasts of AI Risk.

SDO offer a powerful method for explicitly quantifying this uncertainty. To summarise, if you repeatedly sample from the space of all possible analyses of AI Risk then you will sometimes hit a low number for some parameters. The nature of the way conditional probabilities function is that this leads to disproportionately low (asymmetric) risk, which is surprising and unintuitive. An important argument in this essay is that the SDO method is not doing any ‘work’ – rather the method offers a way to think about uncertainty in parameter estimates to help us overcome our cognitive bias. It is rather nice that SDO are rationalist luminaries, but the method would be appropriate even if they had never commented on AI Risk.

I argue that for most individuals, not much will change as a result of this analysis. Almost nobody would have said their certainty over AI Risk scenarios was better than order-of-magnitude, so the finding in this essay that the risk of this kind of Catastrophe is actually towards the lower end of the order-of-magnitude we thought it was is probably not wholly transformative news. On the other hand, there may well be some actionable insight for funding bodies contained within this essay. I’d suggest the three most immediately actionable insights are:

  • We should be devoting significantly more resources to identifying whether we live in a high-risk or low-risk world. The ‘average risk’ (insofar as such a thing actually exists) is sort of academically interesting, but doesn’t help us design strategies to minimise the harm AI will actually do in this world.

  • We should be more concerned with systematic investigation of uncertainty when producing forecasts. In particular, the radical results contained in this essay only hold under quite specific structural assumptions. A considered and systematised approach to structural uncertainty would be a very high-value follow up to this essay about parameter uncertainty, but would need to be written by an expert in AI Risk to move beyond surface-level insight.

  • More generally, the analysis in this essay implies a reallocation of resources away from macro-level questions like, “When will AI be created?” and towards the microdynamics of AI Risk. For example, “What is the probability that the Alignment Problem turns out to be easy?” is the best early differentiator between low-risk and high-risk worlds, but it is a notably under-researched question (at least on a quantitative level).

Overall, ‘Dissolving AI Risk’ is a slightly incendiary title; AI Risk is still a live concern, and even a 1.6% chance of a terrible risk to humanity is too high for comfort. The title is an homage to Sandberg, Drexler and Ord, and their excellent 2018 paper on the Fermi Paradox. The reason for the homage is that this is really an essay about their insight, applied to a fairly straightforward survey dataset that happens – coincidentally—to be about AI Risk. Their insight is that for any application where you are multiplying conditional probabilities, and uncertainty over those probabilities spans at least one order-of-magnitude, you will end up with a significantly asymmetric distribution of underlying risks, favouring low-risk outcomes. This is not at all intuitive, but the extensive sensitivity and scenario analysis here is hopefully enough to make the case that the result is robust (even if I haven’t done a perfect job explaining the SDO mechanism). The overall goal of this essay is to demonstrate a practical example of the use of uncertainty analysis to create novel insight, and to the extent that I have succeeded at ‘dissolving’ AI Risk by an order of magnitude, I hope this essay accomplishes that.

  1. ^

    If you clicked on this footnote because you didn’t totally understand why this would be the case, I will reassure you that there is a lot more explanation to follow in the main body of the essay.

    To help orient you though, an analogy with sports teams might be helpful:

    In a sports league there are multiple teams competing at games which can be modelled roughly as (weighted) coin tosses as to who wins. Losing one game doesn’t mean you lose the whole season, so in general the best team usually wins the League.

    A sports elimination bracket is the same, except if your team loses a single game they are out of the whole tournament. This means that the best team does not always win an elimination bracket – they need to have a certain amount of luck to win every single game in a row.

    So looking only at the best team’s probability of winning one specific game will systematically underrepresent their wins in a league-type format and systematically overrepresent their wins in an elimination-type format. You are much safer betting on the best team to win a league-type format than betting on the best team to win an elimination-type format, all other things being equal.

    Most models of AI risk are – at an abstract enough level – more like an elimination tournament than a league, at least based on what has been published on various AI-adjacent forums. The AI needs everything to go its way in order to catastrophically depower humanity (although for sure it can make things very nasty for humans without catastrophically depowering them). Even if the AI is the ‘best team’ in the elimination tournament – which is a disturbingly apt metaphor now I think about it – simply because it is an elimination tournament the best player is disadvantaged compared to its probable performance in a single match

    If this example confuses more than it enlightens, there is a much more comprehensive explanation to follow.

  2. ^

    During this step I was made aware of the ‘Modeling Transformative AI Risk’ (MTAIR) project, which is a significantly more textured approach to modelling AI Risk, building on the work of Cottier and Shah (2019). This is effectively the next-generation of laying out the logical interrelationship between steps between now and a possible AI Catastrophe, building on the strong foundations of Carlsmith (2021). I am fairly confident that once published it will completely resolve my concerns about structural uncertainty analysis, which is why I make less of a fuss about structural uncertainty here than I did in my earlier essay about GiveWell’s model

  3. ^

    I ended up having to exclude most of Aird’s database because the questions included in the database didn’t quite fit the decision problem the Future Fund were interested in. Nevertheless, Aird’s database deserves significantly more credit for this essay than it is about to get, because I used the estimates that he collated to parameterise a proof-of-concept model I then used to design everything else. In general, I suspect a significant cause of the issues I diagnose with uncertainty analysis in EA spaces are because there are few people like Aird doing hard and mostly thankless work to systematically bring together different perspectives on the same issue. This is a fertile area for high-impact funding, although slightly outside the scope of this essay.

  4. ^

    By which I mean Astral Codex Ten, LessWrong and the Effective Altruism Forums. It was simply a blunder to miss the AI Alignment Forums – I misread my notes. I assumed there was enough cross-pollination between sources that this didn’t matter too much.

  5. ^

    Ho ho

  6. ^

    If anyone disagrees with my adjustment of their results in this way, I would be delighted to bet you $1 that you are wrong at one to a billion odds – please PM me!

  7. ^

    The average here is the geometric mean of odds, although I convert it back into a probability to make it more comparable to the simple mean

    A classic statistician drum to bang is that there is no such thing as ‘an average’ – there are just different measures of central tendency which are more or less appropriate for certain applications.

    In this particular case, a simple mean would be quite misleading, because it implicitly proposes that a 99% and 99.99% probability express basically the same position (the simple mean of – say – 50%, 99% and 99.99% is not that different to the simple mean of – say – 50%, 99% and another 99%). Instead we use geometric mean of odds to ensure that 99.99% is correctly recorded as several orders of magnitude more certain than 99%.

    See here for a really good discussion with further argument and justification

  8. ^

    As an aside, for statisticians: I found method of moment was REALLY bad at generating plausible beta distributions from my real-world data, when previously it has worked pretty well for me and was working perfectly on toy data I was feeding it (eg the Modified Carlsmith numbers I described above). Is that likely to be because the data in this case spans multiple orders of magnitude /​ contains a lot of extreme values? Is there a better method other than grid searching over and over? If anyone has some insight on this problem I can think of a couple of interesting ways to extend my results—please PM me if you’ve ever worked on a problem like this

  9. ^

    Obviously the correct ‘fair betting odds’ depend on the payoff matrix associated with a particular bet. If we set up a bet where you pay $1 and I pay out $X if you are right, then the simple mean is the fair odds for this payoff matrix. If we set up a bet where I pay you $1 for a prediction and you pay me an increasing amount of dollars depending on how overconfident /​ underconfident you were, then the Briar Score (or some other loss function like Log-Loss) gives you the fair betting odds, and this is found with the geometric mean of odds. Edit: Sorry, I have no idea what I mean to say here, please ignore it

    I think either simple mean or geometric mean of odds has a plausible defence for being used in this case, and I’d say I’ve got a weak supposition that geometric mean of odds should be the default. I note however that the Future Fund doesn’t want to get too hung up on what constitutes ‘fair betting odds’, so I haven’t either – this is an essay about distributions not about point estimates.

Froolow18 Oct 2022 22:54 UTC
109 points
63 commentsEA link